Originally a guest post 16 December 2019 at Climate Etc
Introduction
In an earlier article here I discussed the Lewis and Curry (2018) paper “The impact of recent forcing and ocean heat uptake data on estimates of climate sensitivity” (LC18) and set out its results. The LC18 analysis used a global energy budget model to estimate the planetary equilibrium climate sensitivity (ECS) and transient climate response (TCR). ECS and TCR are estimated from changes (Δ) in global mean surface temperature [T], effective radiative forcing (ERF) [F] and the planetary radiative imbalance[1] [N] between a base and a final period, as:
ECS = F2×CO2 × ΔT /(ΔF – ΔN) and TCR = F2×CO2 × ΔT /ΔF
where F2×CO2 is the ERF for a doubling of atmospheric CO2 concentration.
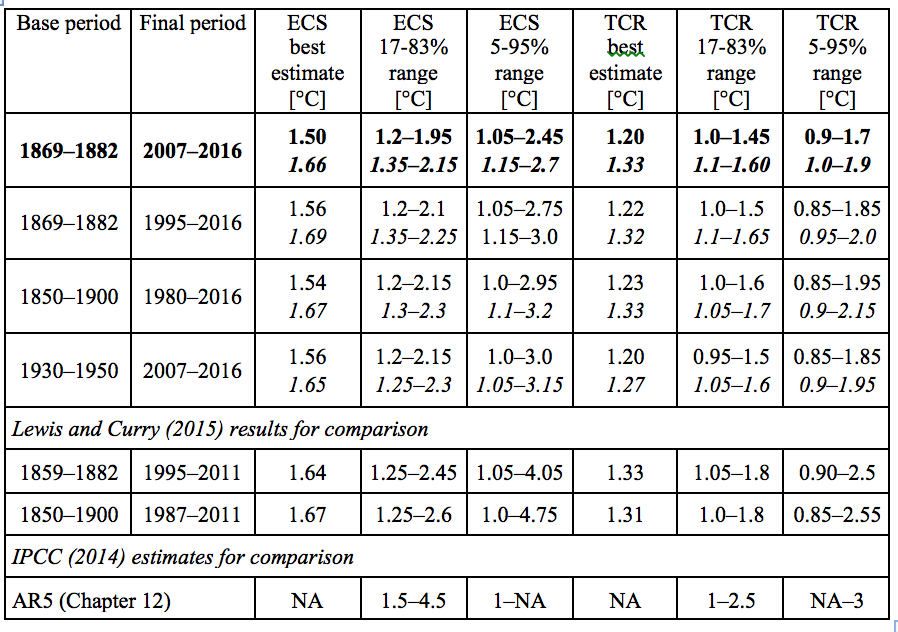
The main LC18 estimates for ECS and TCR were as per Table 1. The main points of note are that they lie near the bottom end of the IPCC AR5 ‘likely’ ranges for ECS and TCR, and that they are both less uncertain and slightly lower than those given in the predecessor study, Lewis & Curry (2015) when using HadCRUT4 global surface temperature data. The LC18 best estimates based on the faster warming infilled Cowtan & Way Had4_krig_v2 temperature dataset are very similar to the HadCRUT4-based results in Lewis & Curry (2015).
Table 1 (based on Table 3 in LC18) Best estimates (medians) and uncertainty ranges for ECS and TCR using the base and final periods indicated. Values in roman type compute the temperature change involved (ΔT) using the HadCRUT4v5 dataset; values in italics compute using the infilled, globally-complete Had4_krig_v2 (Cowtan & Way) dataset. The preferred estimates are shown in bold. Ranges are stated to the nearest 0.05 K. Also shown are the comparable results (using the HadCRUT4v2 dataset) from LC15 for the first two period combinations given in that paper. ECS estimates assume that effective climate sensitivity does not change with time elapsed since imposition of forcing.
Summary of the Comment and Reply
A Comment on LC18 by Kevin Cowtan and Peter Jacobs, and a Reply from myself and Judith Curry, have just been published by Journal of Climate. A copy of the Reply is available here.
The Comment (CJ20) is arguably more a critique of observational sea surface temperature (SST) datasets than of the methods and results of LC18. Its abstract reads as follows:
Lewis and Curry (2018) (hereafter LC18) present a method for the estimating the transient climate response (TCR) of the climate system from the temperature change between two time windows – an early baseline period in the 19th century, and a modern period primarily in the 21st century. The results suggest a lower value of TCR than estimates from climate model simulations. Previous studies have identified uncertainty in the historical forcings, the impact of the time evolution of the forcing on temperature response, and observational issues as contributory factors to this disagreement. We investigate a further factor: uncertainty in the bias corrections applied to historical sea surface temperature data. This uncertainty can particularly impact the estimation of variables on decadal timescales, and therefore impact the estimation of TCR using the window method as well as estimates of internal variability. We demonstrate that use of the whole historical record can mitigate the impacts of working with short time windows to some extent, particularly with respect to the early part of the record.
Originally, CJ20 asserted that the base and final periods – what they call early and late windows – chosen in LC18 – which were matched as regards volcanic forcing and influence from multidecadal internal variability – led to lower values of TCR (CJ20 did not address the LC18 ECS estimates). They subsequently removed that claim, which the analysis in our submitted Reply disproved. The final version of CJ20 focuses on the possible impact of using windows rather than all the historical data, in particular the impact – based on comparing warming in CMIP5 (current generation) climate models and in observations – of the choice of varying dates for the windows, and on uncertainty in bias corrections to historical SST data. CJ20 focus on use of the HadCRUT4 temperature record, but – as LC18 made clear – it is appropriate to use a globally complete record for comparison with climate model results. We accordingly used only Kevin Cowtans’s infilled version of HadCRUT4, Had4_krig_v2, in our Reply.
The abstract for my and Judith Curry’s Reply to CJ20 reads as follows:
Cowtan and Jacobs assert that the method used by Lewis and Curry in 2018 (LC18) to estimate the climate system’s transient climate response (TCR) from changes between two time windows is less robust – in particular against sea surface temperature bias correction uncertainty – than a method that uses the entire historical record. We demonstrate that TCR estimated using all data from the temperature record is closely in line with that estimated using the LC18 windows, as is the median TCR estimate using all pairs of individual years. We also show that the median TCR estimate from all pairs of decade-plus length windows is closely in line with that estimated using the LC18 windows, and that incorporating window selection uncertainty would make little difference to total uncertainty in TCR estimation. We find that when differences in the evolution of forcing are accounted for, the relationship over time between warming in CMIP5 models and observations is consistent with the relationship between CMIP5 TCR and LC18’s TCR estimate, but fluctuates due to multidecadal internal variability and volcanism. We also show that various other matters raised by Cowtan and Jacobs have negligible implications for TCR estimation in LC18.
In a nutshell, we refuted all points of substance made in CJ20. I plan to deal with the differences between observed and CMIP5 model-simulated historical warming, which formed the basis of CJ20’s numerical analysis, in a subsequent article. In this article, I will elaborate on our refutation of points in the remainder of CJ20.
Window selection related uncertainty
Regarding the claim by CJ20 concerning uncertainty induced by window choice, this is what we had to say in the Reply, having tested the effects of random selection of windows from a decade upwards in length,[2] all of which led to median TCR estimates very close to LC18’s 1.33 °C [= 1.33 K]:
For estimates with the highest (2.0 Wm−2) minimum forcing increase, which are most relevant to LC18’s TCR estimate, the 5–95% TCR uncertainty range arising from random window selection is 1.08–1.54 K, or 1.20–1.59 K using 0.55-scaled volcanic forcing. The width of these ranges – 0.103 and 0.073, respectively, in fractional standard deviation terms[3] – reflects the fact that many of the window combinations involve mismatched influences from internal variability and/or volcanism. These window selection uncertainty ranges do not imply that LC18 underestimated uncertainty in global temperature change: the 1σ fractional uncertainty in LC18’s preferred TCR estimate attributable to temperature change uncertainty (including that from internal variability) alone was 0.103.[4] Moreover, even if no allowance is made for double counting of temperature change uncertainty, estimated overall TCR uncertainty would increase little if window selection uncertainty were added. Adding (in quadrature) the 0.103 or 0.073 1σ fractional uncertainty in TCR from window selection to the 1σ fractional uncertainty of the preferred LC18 TCR estimate, would only increase it to 1.13⤬ its original level, or to 1.07⤬ that level if using 0.55-scaled volcanic forcing.[5]
This shows that uncertainty in TCR estimation arising from window selection is minor even if no allowance is made for double counting of temperature uncertainty, and negligible if allowance is made for such doubling counting.
Using data from the entire historical record
CJ20 propose use of data from the entire historical record. In fact, LC18 tested doing so, by the usual regression method, but found mismatching volcanic influence made estimation sensitive to the scaling factor used for volcanic forcing. Without scaling down volcanic forcing the TCR estimate from regression over the whole historical period is far lower than that from using the windows method. This is what we said in the Reply:
When AR5 volcanic forcing is scaled by 0.55, regression of median annual-mean temperature on forcing over 1850–2016 gives a 1.27 K Had4_krig_v2-based TCR estimate, marginally lower than LC18’s 1.33 K two-window based preferred estimate. Regressing pentadal means (over 1852–2016) significantly improves the fit (to an R2 of 0.92) and gives a TCR estimate of 1.33 K. Using such pentadal-mean regression on each of the 500,000 pairs of samples of temperature and forcing time series gives a 5–95% TCR range of 0.91–1.84 K, marginally lower and narrower than the LC18 preferred estimate range.
So, the results of TCR estimation using data from the entire historical record is closely in line with those using LC18’s window method and chosen windows, provided the volcanic forcing is scaled down as per LC18’s recommendation. However, the uncertainty induced by having to estimate the appropriate volcanic forcing scaling factor arguably makes using data from the full historical record a less satisfactory approach than using the windows method.
Issues with historical sea surface temperature data
There is indeed significant uncertainty as to the accuracy of the global SST record. However, CJ20 did not show that the LC18 TCR estimates were materially affected by any identified errors in SST bias corrections. Nor did they show that uncertainty in the SST record was greater than that estimated by the providers of the datasets used in LC18.
CJ20 make the point that coverage of the ‘water hemisphere’ was almost non-existent in the 1860s. However, the 1869–82 primary early window used in LC18 avoids the 1860s (save for 1869, when coverage was better), and provides slightly higher coverage in the (land-sparse) southern hemisphere than in the northern hemisphere.
CJ20 also state that nineteenth century temperatures are dependent on large ‘bucket corrections’ to sea surface temperature (SST) observations, however CJ20 themselves suggest that the change from wooden buckets to poorly insulated canvas buckets requiring a large bias correction occurred primarily during 1890–1910. Bucket corrections were relatively small during 1869–82, the LC18 early window.
Possible misestimation of forcings
This is what we wrote in the Reply concerning two forcing estimation issues raised in CJ20:
CJ20 claim that previous studies have identified differences in inferred forcings and in the temperature impact of historical versus transient forcing changes as potential explanatory factors for recent observational energy-budget TCR estimates being lower than average climate model TCR values. None of the three supporting studies that they cite supports either contention.
and
CJ20 claim that comparison of modeled and observed temperatures for late windows starting after 2005 is affected by overestimation of forcings in models. Since LC18 did not make any comparisons of modeled and observed temperatures over the historical period, the only issue of relevance to LC18 is whether it misestimated recent forcing. None of the three supporting studies that CJ20 cite indicate that LC18 misestimated recent forcing.
In fact, a more comprehensive study[6] found, in their CMIP5-specification historical simulations, that since the mid-2000s underestimation of changes in other forcing agents more than counteracted overestimation of changes in solar and volcanic forcing. Moreover, none of the studies cited in CJ20 addressed the real problem, of bias in CMIP5 model forcing that already existed several decades ago (due to principally to excessive aerosol forcing); none of their analyses started before 1980.
Ocean and air surface temperature in models and observations
In CMIP5 models near-surface marine air temperature warms more than the ocean surface temperature field (‘tos‘). CJ20 state that “Lewis and Curry argue that this field [tos] is not the top layer of the bulk ocean surface temperature” (to which measured SST broadly corresponds). However, this straw man argument, which CJ20 disprove, was never made in LC18. As the reply states:
CJ20’s claim that LC18 “argue that this field [tos] is not the top layer of the bulk ocean surface temperature” is incorrect. Rather, LC18 argued that the tas/tos warming difference reflects the model-simulated warming difference between tas and ocean skin temperature, which will warm differently from SST.
There are theoretical reasons for expecting air just above the ocean surface to warm slightly faster than the ocean skin temperature. However, the extent of the difference depends on many factors and is uncertain, as is the difference between the warming rates of SST and of ocean skin temperature. LC18 therefore focused on observational rather than CMIP5 model evidence in this area. We say in the Reply:
LC18 (section 7e) concluded from observational and reanalysis evidence that in the real climate system, tas warmed at most a few per cent more than a blend of tas and tos (model top ocean layer temperature), a substantially smaller difference than that claimed by CJ20. Indeed, the 1979-onwards ERA-interim reanalysis globally-complete surface air temperature record, adjusted for inhomogeneities in their SST source (Simmons et al. 2017), shows slightly lower warming over 1979–2016 than does Had4_krig_v2.
It is also worth noting that in CMIP5 models tas, unlike tos, is a diagnostic rather than a prognostic variable – it is a parameterised extraneous variable, not a variable featuring in the basic model physics.
Conclusion
None of the criticisms of LC18 in the Reply stand up to examination. I leave examination of differences between observed and CMIP5 model-simulated historical warming, which formed the basis of CJ20’s numerical analysis, to a subsequent article. Suffice to say here that such differences, when properly analysed in the light of differences in forcing evolution, are fully consistent with the LC18 TCR estimate.
Nicholas Lewis 16 December 2019
[1] N is estimated from its counterpart, the rate of climate system heat uptake, which is mainly by the ocean.
[2] Since small inter-window forcing increases provide poor TCR estimation, minimum required inter-window forcing increases, ranging from 1.0 to 2.0 Wm−2, were imposed. (The greater the forcing increase the lower the relative uncertainty, as regards both forcing and the change in temperature that it causes. The windows used for LC18’s main ECS and TCR estimates gave a forcing increase of 2.52 Wm−2.) There were over 11,000 decade plus long window combinations giving a forcing increase of 2.0 Wm−2 or more. For computational tractability, early and late windows were specified to be of equal length. When using LC18’s suggested 0.55 scaling of volcanic forcing the median TCR estimates were even closer to 1.33 K at all levels of required forcing increase, and had lower uncertainty ranges, than when using unscaled volcanic forcing.
[3] So as to be able readily to combine uncertainties, we work with 1 standard deviation fractional uncertainties, here derived by scaling from 17-83% ranges and medians in Table 1
[4] Scaling from the 5-95% range and median for Had4_krig_v2 ΔT in Table 2 of LC18. If temperature uncertainty alone is incorporated, the fractional uncertainty in TCR equals that in ΔT.
[5] Scaling from the 17-83% range in Table 3 of LC18, giving a fractional standard deviation of 0.193 for the preferred LC18 TCR estimate. Uncertainties are taken to be normally distributed and independent for the purposes of deriving their standard deviations and combining them. Adding in quadrature a fractional standard deviation of 0.103 (0.073) to the original level of 0.193 increases it to 0.219 (0.207).
[6] Outten, S., Thorne, P., Bethke, I. and Seland, Ø., 2015. Investigating the recent apparent hiatus in surface temperature increases: 1. Construction of two 30‐member Earth System Model ensembles. Journal of Geophysical Research: Atmospheres, 120(17), pp.8575-8596.
Leave A Comment