Originally a guest post October 17, 2019 at Climate Audit.
The recently published open-access paper “How accurately can the climate sensitivity to CO2 be estimated from historical climate change?” by Gregory et al.[i] makes a number of assertions, many uncontentious but others in my view unjustified, misleading or definitely incorrect. Perhaps most importantly, they say in the Abstract that “The real-world variations mean that historical EffCS [effective climate sensitivity] underestimates CO2 EffCS by 30% when considering the entire historical period.” But they do not indicate that this finding relates only to effective climate sensitivity in GCMs, and then only to when they are driven by one particular observational sea surface temperature dataset.
However, in this article I will focus on one particular statistical issue, where the claim made in the paper can readily be proven wrong without needing to delve into the details of GCM simulations.
Gregory et al. consider a regression in the form R = α T, where T is the change in global-mean surface temperature with respect to an unperturbed (i.e. preindustrial) equilibrium, and R = α T is the radiative response of the climate system to change in T. α is thus the climate feedback parameter, and F2xCO2 / α is the EffCS estimate, F2xCO2 being the effective radiative forcing for a doubling of preindustrial atmospheric carbon dioxide concentration.
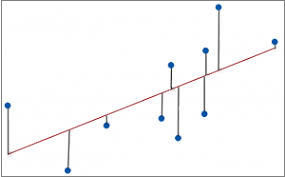
The paper states that “that estimates of historical α made by OLS [ordinary least squares] regression from real-world R and T are biased low”. OLS regression estimates α as the slope of a straight line fit between R and T data points (usually with an intercept term since the unperturbed equilibrium climate state is not known exactly), by minimising the sum of the squared errors in R. Random errors in R do not cause a bias in the OLS slope estimate. Thus in the below chart, with R taken as plotted on the y-axis and T on the x-axis, OLS finds the red line that minimizes the sum of the squares of the lengths of the vertical lines.
However, some of the variability in measured T may not produce a proportionate response in R. That would occur if, for example, T is measured with error, which happens in the real world. It is well known that in such an “error in the explanatory variable” case, the OLS slope estimate is (on average) biased towards zero. This issue has been called “regression dilution”.
Regression dilution is one reason why estimates of climate feedback and climate sensitivity derived from warming over the historical period often instead use the “difference method”.[ii] [iii] [iv] [v] The difference method involves taking the ratio of differences, ΔT and ΔR, between T and R values late and early in the period. In practice ΔT and ΔR are usually based on differencing averages over at least a decade, so as to reduce noise.
I will note at this point that when a slope parameter is estimated for the relationship between two variables, both of which are affected by random noise, the probability distribution for the estimate will be skewed rather than symmetric. When deriving a best estimate by taking many samples from the error distributions of each variable, or (if feasible) by measuring them each on many differing occasions, the appropriate central measure to use is the sample median not the sample mean. Physicists want measures that are invariant under reparameterization[vi], which is a property of the median of a probability distribution for a parameter but not, when the distribution is skewed, of its mean. Regression dilution affects both the mean and the median estimates of a parameter, although to a somewhat different extent.
So far I agree with what is said by Gregory et al. However, the paper goes on to state that “The bias [in α estimation] affects the difference method as well as OLS regression (Appendix D.1).” This assertion is wrong. If true, this would imply that observationally-based estimates using the difference method would be biased slightly low for climate feedback, and hence biased slightly high for climate sensitivity. However, the claim is not true.
The statistical analyses in Appendix D consider estimation by OLS regression of the slope m in the linear relationship y(t) = m x(t), where x and y are time series the available data values of which are affected by random noise. Appendix D.1 considers using the difference between the last and first single time periods (here, it appears, of a year), not of averages over a decade or more, and it assumes for convenience that both x and y are recentered to have zero mean, but neither of these affect the point of principle at issue.
Appendix D.1 shows, correctly, that when only the endpoints of the (noisy) x and y data are used in an OLS regression, the slope estimate for m is Δy/Δx, the same as the slope estimate from the difference method. It goes on to claim that taking the slope between the x and y data endpoints is a special case of OLS regression and that the fact that an OLS regression slope estimate is biased towards zero when there is uncorrelated noise in the x variable implies that the difference method slope estimate is similarly so biased.
However, that is incorrect. The median slope estimate is not biased as a result of errors in the x variable when the slope is estimated by the difference method, nor when there only two data points in an OLS regression. And although the mean slope estimate is biased, the bias is high, not low. Rather than going into a detailed theoretical analysis of why that is the case, I will show that it is by numerical simulation. I will also explain how in simple terms regression dilution can be viewed as arising, and why it does not arise when only two data points are used.
The numerical simulations that I carried out are as follows. For simplicity I took the true slope m as 1, so that the true relationship is y = x, and that true value of each x point is the sum of a linearly trending element running from 0 to 100 in steps of 1 and a random element uniformly distributed in the range -30 to +30, which can be interpreted as a simulation of a trending “climate” portion and a non-trending “weather” portion.[vii] I took both x and y data (measured) values as subject to zero-mean independent normally distributed measurement errors with a standard deviation of 20. I took 10,000 samples of randomly drawn (as to the true values of x and measurement errors in both x and y) sets of 101 x and 101 y values.
Using OLS regression, both the median and the mean of the resulting 10,000 slope estimates from regressing y on x using OLS were 0.74 – a 26% downward bias in the slope estimator due to regression dilution.
The median slope estimate based on taking differences between the averages for the first ten and the last ten x and y data points was 1.00, while the mean slope estimate was 1.01. When the averaging period was increased to 25 data points the median bias remained zero while the already tiny mean bias halved.
When differences between just the first and last measured values of x and y were taken,[viii] the median slope estimate was again 1.00 but the mean slope estimate was 1.26.
Thus, the slope estimate from using the difference method was median-unbiased, unlike for OLS regression, whether based on averages over points at each end of the series or just the first and last points.
The reason for the upwards mean bias when using the difference method can be illustrated simply, if errors in y (which on average have no effect on the slope estimate) are ignored. Suppose the true Δx value is 100, so that Δy is 100, and that two x samples are subject to errors of respectively +20 and –20. Then the two slope estimates will be 100/120 and 100/80, or 0.833 and 1.25, the mean of which is 1.04, in excess of the true slope of 1.
The picture remains the same even when (fractional) errors in x are smaller than those in y. On reducing the error standard deviation for x to 15 while increasing it to 30 for y, the median and mean slope estimates using OLS regression were both 0.84. The median slope estimates using the difference method were again unbiased whether using 1, 10 or 25 data points at the start and end, while the mean biases remained under 0.01 when using 10 or 25 data point averages and reduced to 0.16 when using single data points.
In fact, a moment’s thought shows that the slope estimate from 2-point OLS regression must be unbiased. Since both variables are affected by error, if OLS regression gives rise to a low bias in the slope estimate when x is regressed on y, it must also give rise to a low bias in the slope estimate when y is regressed on x. If the slope of the true relationship between y and x is m, that between x and y is 1/m. It follows that if regressing x on y gives a biased low slope estimate, taking the reciprocal of that slope estimate will provide an estimate of the slope of the true relationship between y and x that is biased high. However, when there are 2 data points the OLS slope estimate from regressing y on x and that from regressing x on y and taking its reciprocal are identical (since the fit line will go through the 2 data points in both cases). If the y-against-x and x-against-y OLS regression slope estimates were biased low that could not be so.
As for how and why errors in the x (explanatory) variable cause the slope estimate in OLS regression to be biased towards zero (provided there are more than two data points), but errors in the y (dependent) variable do not, the way I look at it is this. For simplicity, I take centered (zero-mean) x and y values. The OLS slope estimate is then Σxy / Σxx, that is to say the weighted sum of the y data values divided by the weighted sum of the x data values, the weights being the x data values. An error that moves a measured x value further from the mean of zero not only reduces the slope y/x for that data point, but also increases the weight given to that data point when forming the OLS slope estimate. Hence such points are given more influence when determining the slope estimate. On the other hand, an error in x that moves the measured value nearer to zero mean x value, increasing the y/x slope for that data point, reduces the weight given to that data point, so that it is less influential in determining the slope estimate. The net result is a bias towards a smaller slope estimate. However, for a two-point regression, this effect does not occur, because whatever the signs of the errors affecting the x-values of the two points, both x-values will always be equidistant from their mean, and so both data points will have equal influence on the slope estimate whether they increase or decrease the x-value. As a result, the median slope estimate will be unbiased in this case. Whatever the number of data points, errors in the y data points will not affect the weights given to those data points when forming the OLS slope estimate, and errors in the y-data values will on average cancel out when forming the OLS slope estimate Σxy / Σxx.
So why is the proof in Gregory et al. Appendix D.1, supposedly showing that OLS regression with 2 data points produces a low bias in the slope estimate when there are errors in the explanatory (x) data points, invalid? The answer is simple. The Appendix D.1 proof relies on the proof of low bias in the slope estimate in Appendix D.3, which is expressed to apply to OLS regression with any number of data points. But if one works through the equations in Appendix D.3, one finds that in the case of only 2 data points no low bias arises – the expected value of the OLS slope estimate equals the true slope.
It is a little depressing that after many years of being criticised for their insufficiently good understanding of statistics and lack of close engagement with the statistical community, the climate science community appears still not to have solved this issue.
Update 29 October 2019
Just to clarify, the final paragraph is a general remark about the handling of statistical issues in climate science research, not a particular remark about this new paper (where the statistical mistake made does not in any case affect any of the results).
[i] Gregory, J.M., Andrews, T., Ceppi, P., Mauritsen, T. and Webb, M.J., 2019. How accurately can the climate sensitivity to CO₂ be estimated from historical climate change?. Climate Dynamics.
[ii] Gregory JM, Stouffer RJ, Raper SCB, Stott PA, Rayner NA (2002) An observationally based estimate of the climate sensitivity. J Clim 15:3117–3121.
[iii] Otto A, Otto FEL, Boucher O, Church J, Hegerl G, Forster PM, Gillett NP, Gregory J, Johnson GC, Knutti R, Lewis N, Lohmann U, Marotzke J, Myhre G, Shindell D, Stevens B, Allen MR (2013) Energy budget constraints on climate response. Nature Geosci 6:415–416
[iv] Lewis, N. and Curry, J.A., 2015. The implications for climate sensitivity of AR5 forcing and heat uptake estimates. Climate Dynamics, 45(3-4), pp.1009-1023.
[v] Lewis, N. and Curry, J., 2018. The impact of recent forcing and ocean heat uptake data on estimates of climate sensitivity. Journal of Climate, 31(15), pp.6051-6071.
[vi] So that, for example, the median estimate for the reciprocal of a parameter is the reciprocal of the median estimate for the parameter. This is not generally true for the mean estimate. This issue is particularly relevant here since climate sensitivity is reciprocally related to climate feedback.
[vii] There was an underlying trend in T over the historical period, and taking it to be linear means that, in the absence of noise, linear slope estimated by regression and by the difference method would be identical.
[viii] Correcting the small number of negative slope estimates arising when the x difference was negative but the y difference was positive to a positive value (see, e.g., Otto et al. 2013). Before that correction the median slope estimate had a 1% low bias. The positive value chosen (here the absolute value of the negative slope estimate involved) has no effect of the median slope estimate provided it exceeds the median value of the remaining slope estimates, but does materially affect the mean slope estimate.
Leave A Comment