A pdf copy of this article is available here
Introduction
Readers may recall my articles in 2018 about statistical flaws in a Nature paper that claimed to show ocean warming was greater than generally thought[1]. That paper was subsequently retracted. Nature tends to publish papers that use novel approaches and/or provide newsworthy results, which have not yet stood the test of time. Given that background, and that peer review often fails to spot problems with methods or calculations, I read Nature papers with particular care. Helpfully, Nature makes peer review files available, unlike most journals. Although Nature does not also make the submitted version available, unlike the EGU Open Access journals, authors are increasingly posting open-access preprints when submitting manuscripts to journals, thus revealing changes made during peer review or after acceptance.
This article concerns the paper “Globally resolved surface temperatures since the Last Glacial Maximum” by Matthew Osman et al.[2] (hereafter Osman 2021) published by Nature in November 2021. Its Abstract reads:
Climate changes across the past 24,000 years provide key insights into Earth system responses to external forcing. Climate model simulations and proxy data have independently allowed for study of this crucial interval; however, they have at times yielded disparate conclusions. Here, we leverage both types of information using paleoclimate data assimilation to produce the first proxy-constrained, full-field reanalysis of surface temperature change spanning the Last Glacial Maximum to present at 200-year resolution. We demonstrate that temperature variability across the past 24 thousand years was linked to two primary climatic mechanisms: radiative forcing from ice sheets and greenhouse gases; and a superposition of changes in the ocean overturning circulation and seasonal insolation. In contrast with previous proxy-based reconstructions our results show that global mean temperature has slightly but steadily warmed, by ~0.5 °C, since the early Holocene (around 9 thousand years ago). When compared with recent temperature changes, our reanalysis indicates that both the rate and magnitude of modern warming are unusual relative to the changes of the past 24 thousand years.
Matthew Osman kindly sent me a copy of the paywalled paper; the submitted version preprint is available here. The significance of this topic relates both to the use of Last Glacial Maximum (LGM) to preindustrial global temperature change to estimate climate sensitivity, and the magnitude and causes of temperature variability since the LGM, including in particular how preindustrial global temperature compares with that in the early Holocene.
Osman 2021 reconstructed time-series of global, spatially-resolved surface temperatures from the LGM period some 20,000 or so years ago to the preindustrial late Holocene, through extending data-assimilation methods developed by its second author, Jessica Tierney, and used by her in a 2020 paper to spatially reconstruct LGM temperatures[3] (hereafter Tierney 2020).
Although Tierney 2020 states that best estimates of the LGM global mean surface air temperature (GMAT)[4] change relative to preindustrial ranged from −1.7°C to −8.0°C, most were between −3.0°C and −6.0°C. For what it is worth, in the two most recent global climate model (GCM) generations simulated preindustrial-to-LGM GMAT change varied from –2.7°C to −5.4°C and from −3.3°C to −7.2°C.[5] Tierney 2020 estimated the preindustrial to LGM GMAT change (from the stable period 19,000 to 23,000 years ago) to be −5.9°C, with a tight −6.3°C to −5.6°C 95% uncertainty range. Osman 2021 go further, estimating that change as −6.8 ± 1.0 °C (95% uncertainty range)[6]. Surprisingly, given the very similar methodology and proxies they used, their two estimates are almost statistically inconsistent.[7]
Both Osman 2021 and Tierney 2020 used a large selection of four types of sea surface temperature (SST) proxies; no land or deep ocean proxies were used. It appears that the 539 proxies used by Osman 2021 – which sought long-record, time resolved proxies to enable reconstruction over the whole LGM to preindustrial period – were largely a subset of the 955 LGM and 880 late Holocene proxies used in Tierney 2020. Proxy coverage in the central Pacific ocean, which was very limited in Tierney 2020 with one proxy near the equator and one each in the north and south, is non-existent in Osman 2021. It is unclear why those three proxies, which were common to the LGM and late Holocene periods, were not used in Osman 2021.
Osman 2021’s proxy-only reconstruction
In addition to their main data-assimilation reconstruction (“LGMR”), Osman 2021 produced a proxy-only reconstruction. I will start by examining that. They estimate local SST from proxy data, a process subject to substantial uncertainty and possible bias.[8] By binning these local SST estimates by age-range and latitude-band, they derive mean 60°S−60°N SST at 200 year resolution and scale this to give an estimated GMAT time series.[9] This well established procedure inevitably involves uncertainty and possible bias. However, unlike with the data-assimilation method, the resulting GMAT estimates are not dependent on the spatial and temporal accuracy of paleoclimate simulations by a single GCM, which may well be poor.
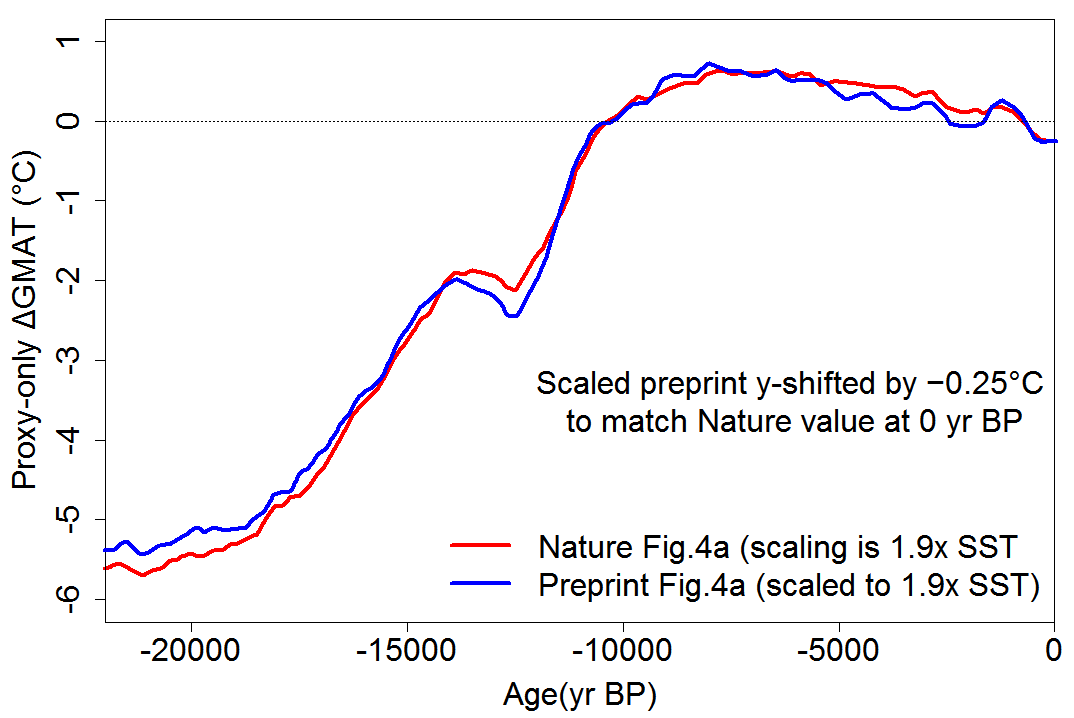
Fig. 4 of their Nature paper shows the Osman 2021 proxy-only reconstruction, over 0–22,000 yr BP[10] in panel a and, enlarged, over 500–11,000 yr BP in panel b. Helpfully, Nature makes the underlying plot data available. Unfortunately, there are at least two errors in panel b. First, the dotted lines connecting the time-axes of panels a and b are incorrect; they wrongly imply that panel b covers 0–10,600 yr BP. Secondly, Fig. 4b show a value of −0.46°C for 11,000 BP but no such data point exists[11], while the Fig. 4b plot data is shown as starting at 500 yr BP but actually starts at 100 yr BP.
Of greater concern, the Fig. 4a full period proxy-only reconstruction in Nature differs in shape from the version in their preprint. Figure 1 compares the two versions, matched at age 0, with identical SST to GMAT scaling factor of 1.90.[12] (The actual mean scaling factor used in the preprint was much higher at 2.44, but that was obviously inappropriate.[13]) The Nature version shows a larger temperature change between the LGM and the early Holocene, and less pronounced short term fluctuations. For example, the dip between 12,000 and 13,000 yr BP is much smaller, and the temperature decline between 5,000 and 1,000 yr BP is much more even. This may indicate added smoothing, but that can’t be the whole explanation. It is unclear from the Methods descriptions in the preprint and Nature versions of the paper why their proxy-only reconstructions differ.[14] I wrote to Matthew Osman asking about this but received no reply. It seems surprising that the authors changed their proxy-only reconstruction without making any mention of doing so in any of their peer review responses.
Fig 1. Osman 2021 Nature and preprint Fig. 4a proxy-only reconstructions compared
.
In the absence of a satisfactory justification for these differences, I give more credence to the preprint proxy-only reconstruction. As the two versions of Osman 2021 Fig. 4a show, that matches a scaled version of the well-established Shakun-Marcott Curve (SMC) reconstruction considerably more closely between 14,000 and 1,000 yr BP than does the Nature version.
When applying the 1.90 mean 60°S−60°N SST scaling factor, as per the Nature paper, to the preprint proxy-only reconstruction, the mean GMAT over the stable period 19,000 to 23,000 years ago (commonly used to represent the LGM) is 5.0°C cooler than that over the last 600 years, which appears to be a suitable measure of preindustrial GMAT[15].
However, the 1.90 scaling factor appears excessive. It reflects the mean ratio of GSAT to 60°S−60°N SST in PMIP2 and PMIP3 GCM simulations of the LGM.[16] PMIP2 simulations are very dated. The corresponding mean from PMIP3 simulations alone was 1.84.[17] Moreover, published results from the more recent PMIP4 simulations, involving a larger ensemble of more advanced models with updated estimates of ice sheet configurations and other boundary conditions, show a mean ratio of GSAT to 60°S−60°N ocean surface air temperature of 1.64, 6% lower than that for PMIP3.[18] That points to reducing the PMIP3 derived 1.84 ratio of GSAT to 60°S−60°N SST to 1.73. Applying that PMIP4 ratio to the Osman 2021 preprint proxy-only reconstruction would reduce the preindustrial to LGM GSAT change to −4.6°C, as compared with −4.85°C using the PMIP3 ratio of 1.84. All these estimates are of course subject to substantial uncertainty.
In GCMs, ocean surface air temperature changes more than SST, however the best estimate per the IPCC AR6 report is that changes in SST and in ocean surface air temperature are the same[19]. On that basis, the PMIP4 derived scaling ratio of 1.64 from 60°S–60°N ocean surface air temperature to GMAT changes can be applied directly to SST changes. Applying that ratio to the Osman 2021 preprint proxy-only reconstruction would reduce the preindustrial to LGM GSAT change to −4.3°C.
Osman 2021’s data-assimilation reconstruction (LGMR)
The data-assimilation method used involves, in essence, simulating the global climate at suitable dates using a GCM and then modifying the simulation values at each spatial grid location, statistically interpolated to each 200 year reconstruction time step period[20], by reference to the difference between all proxy values relevant to that time step and the interpolated simulation values at the proxy locations. Their method implements a ‘Kalman filter’ update.
The extent of the modification made at each grid point depends on the covariance across an ensemble of ‘model priors’, representing means of 50 year GCM simulation time slices, of temperatures at that grid-point with those at all sites where proxy values at or close to the same date exist. It also depends, inversely, on sum of the covariance of the simulated values and scaled-down uncertainty in the proxy values. Unfortunately, Osman 2021 does not show the ensemble-mean model prior, nor the difference between it and the LGMR reconstruction, either as a global mean time series or as a map at the LGM. It is therefore not possible to tell to what extent the model prior has been modified in producing the reconstruction.[21]
As well as, like the proxy-only reconstruction, depending on the accuracy of the proxy-derived local SST estimates, the accuracy of the LGMR data-assimilation reconstruction therefore depends critically on the realism of the GCM simulations used and of the spatial covariance structure that they produce. The covariances used appear to be applicable to multidecadal internal variability in the GCM used, and may be different to those applicable to longer term forced climate change.[22]
Data assimilation is a technique suited to cases where observational evidence is abundant and reasonably accurate, with modest uncertainty, and where in addition the model simulations used are known to represent spatiotemporal changes and their covariance reasonably well. In such cases the reconstruction should be dominantly determined by information from the observations. However, none of those conditions are satisfied at the LGM.
When observational evidence is limited and highly uncertain and/or model covariances are low, a data assimilation reconstruction will largely represent model simulation values. It is therefore relevant to note that the model used by Osman 2021, iCESM1.2[23], has a particularly high preindustrial to LGM change in GMAT. The main, CESM1.2, PMIP4 model cooled by 6.8°C, over 2°C more than the PMIP4 average.
It is moreover not entirely clear that the iCESM1.2 model used had been adequately equilibrated before the simulations were carried out: the two preindustrial simulation ensembles listed in Extended Data Table1 had mean GMSTs with ranges that were narrow (14.03–14.25°C and 13.22–13.33°C) but differed by almost 1°C[24].
The Osman 2021 preprint Extended Data Figure 6 gives some indication of the LGMR reconstruction’s dependence on the model-simulation prior. It shows that in many cases best-estimate LGMR GMAT changes exceed those per both the model simulation prior and the proxy-only reconstruction, even before correcting the erroneously high 2.44 60°S−60°N SST to GMAT scaling factor used for the preprint proxy-only reconstruction. Since that scaling factor is far lower in the iCESM1.2 model used, larger LGMR changes than for either the model prior or the proxy-only reconstruction suggest strong dependence of the LGMR GMAT on model-simulated SST changes at the proxy locations generally being lower than their average for the latitude involved (so that proxy changes are larger than those per the model simulation at the same location). However, no evidence is provided as to why that would be the case.
Worryingly, the LGMR results presented in Nature differ from those in the preprint, with cooling at the onset of deglaciation 0.2°C greater in the Nature version. Moreover, the spatial cooling between 9 kyr and 2 kyr shown in the two Osman 2021 Figure 2 versions differs substantially. I could not spot any mention in the peer review files of changes being made.
Validating the LGMR data-assimilation reconstruction
It is impossible to properly verify the spatiotemporal accuracy of the model simulations used, however Osman 2021 do carry out some, albeit limited, validation tests of their LGMR reconstruction. Their ‘external validation’ consists of comparing the LGMR (posterior) Δδ18Op values, and also the model simulation (prior) values, at the proxy locations, with independent ice core and cave speleothem proxy record data. This is similar to the validation test undertaken by Tierney 2020.
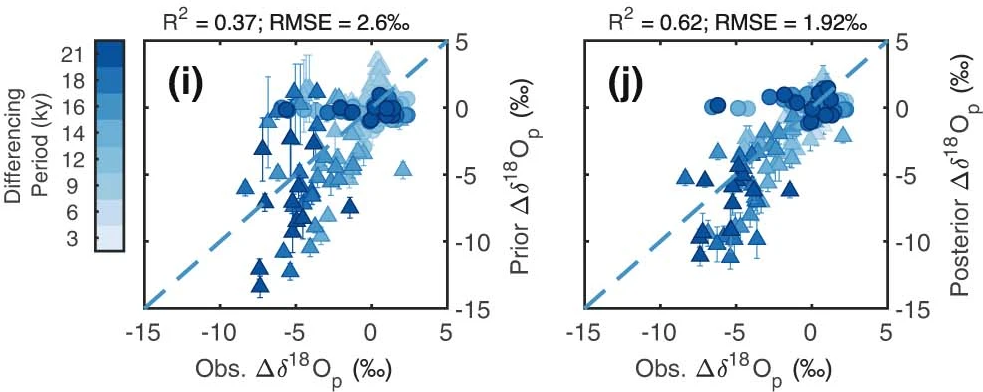
Osman 2021 claim that their external validation test indicates that LGMR substantially improves over the model prior, with the 62% of the variance in the independent records explained by LGMR against 37% by the model prior (simulation values). That is, the R2 improves from 0.37 to 0.62, as shown in Figure 2. This is the final, Nature, version. Oddly, it is not identical to the preprint version, without any mention in the peer review file of any changes being made.
Fig 2. Reproduction of Osman 2021 Extended Data Fig. 3(i)&(j). Triangles represent ice core values and circles represent cave speleothem values, relative to preindustrial, for each Differencing period (simulation time slice). ‘Prior’ refers to the model simulation values. ‘Posterior’ refers to LGMR reconstruction values.
However, Δδ18Op values for different differencing periods are not independent, since changes from preindustrial to any time slice except the final, 3 kyr BP, period will include changes since later time slices. An even more serious concern is that combining the ice core and cave speleothem proxies when estimating the explained variance will artificially increase the proportion of variance explained, since they/their locations evidently have very different sensitivities to temperature changes between preindustrial and the LGM.[25] Osman 2021’s claimed model prior R2 of 0.37, and higher LGMR posterior R2 of 0.62, are spurious, misleading figures.
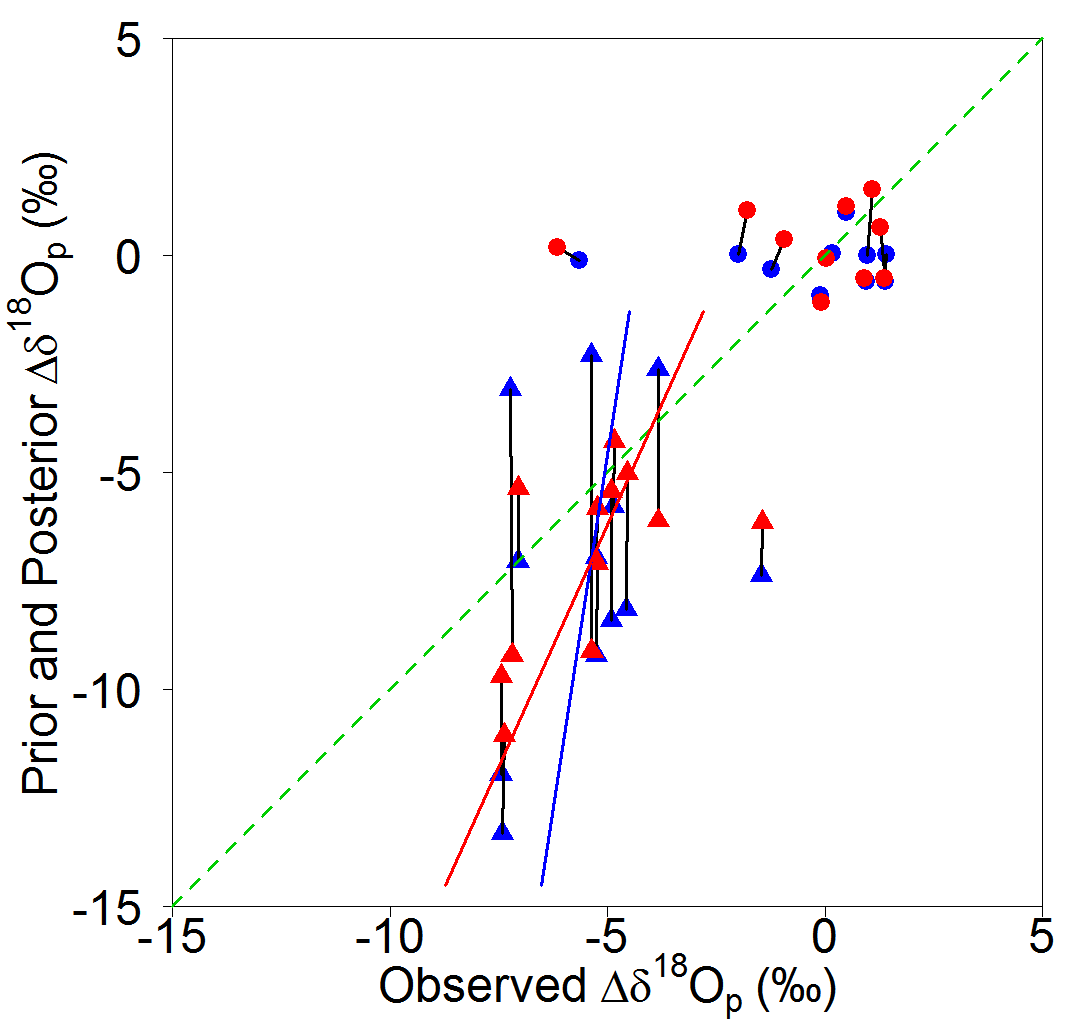
A fairer test would be to consider changes only over the longest differencing period, that between preindustrial and 21 kyr BP[26], and to analyse the ice core and speleothem datasets separately. To clarify the data concerned, Figure 3 shows 21 kyr BP minus preindustrial differences for the model simulations (Prior: blue symbols) and the LGMR reconstruction (Posterior: red symbols), plotted against the co-located proxy (Observed) values.
Fig 3. Ice core values (triangles) and cave speleothem values (circles) for the 21 kyr differencing period, digitized from Osman 2021Extended Data Fig. 3(i)&(j). Blue symbols show model simulation (Prior) values. Red symbols show LGMR reconstruction (Posterior) values. Observed values are in both cases shown along the x-axis. The blue and red lines show the best fit for Observed values when predicted by (regressed on) respectively the model Prior and the LGMR reconstruction Posterior values. The black lines join Prior and Posterior points with the same ordering of Observed (x) digitized values in Extended Data Fig. 3(i) and Fig. 3(j) respectively.
Ice core proxy validation results
For the ice core records, the ordered Observed (x) values from Extended Data Fig. 3(i) (Prior) and Fig. 3(j) (Posterior) are all identical within digitization error (max 0.05‰), with the black lines joining the Prior and Posterior y-values being vertical, as should be the case. The data-assimilation method changes the model simulation values, but it cannot change the observed proxy values.
The best fit when predicting observed values from the model prior ice core values (blue line) explains a negligible proportion of variance (R2 = 0.09; adjusted R2 < 0). The best fit when predicting observed values from the LGMR posterior ice core values (red line) is better, but it is not statistically significant (p >0.05) and it only explains a minority of the variance (R2 = 0.32; adjusted R2 = 0.25). Moreover, the slopes of the best fits are in both cases far from a 1-to-1 relationship through the origin (green dashed line) , albeit less so for the LGMR posterior.
A large majority of the model prior values, and of the LGMR posterior values, show larger changes than the observed values. The mean observed Δδ18Op value is −5.4‰, while the model prior mean is a third larger at −7.2‰ and the LGMR posterior mean is almost as large at 7.0‰. Thus, both the model prior and the LGMR posterior substantially overestimate mean LGM cooling at the ice core locations, by respectively 33% and 31%[27]. Interestingly, if the −6.8°C preindustrial to LGM change in GMAT per the LGMR posterior were scaled down by 1/1.31, it would become −5.2°C, quite close to the change implied by the proxy-only reconstruction.
Cave speleothem proxy validation results
Observed cave speleothem values have a negligible correlation with either prior or posterior values (R2 < 0.001). That provides no support for the validity of either the model simulations or the LGMR reconstruction.
Moreover, a majority of the ordered cave speleothem proxy record values in Extended Data Fig. 3(j) do not match those in Fig. 3(i) within 0.1‰, double the digitization error, as shown by the black lines joining the circles not being vertical in some cases. The most negative Observed cave speleothem (leftmost dark blue circle in each of panels (i) and (j) of the original figure ) values are glaringly different: −5.65‰ and −6.15‰: a discrepancy of 0.5‰ , ten times digitization error. This cannot possibly be correct. Something has evidently gone seriously wrong here, and a correction by Osman and co-authors appears to be required.
Other tests
Osman 2021 also show results for what they call ‘internal validation testing’ using values for 20% of their proxies randomly withheld at each time step. However, this appears to be a weak test; most of their proxies have nearby other proxies. Moreover, as they say, the U-shaped (rather than flat) rank histogram indicates a lack of structural variance in the model prior. Tierney 2020 carried out a similar analysis, but did not claim that the results validated their LGM reconstruction. Indeed, Osman 2021 seemingly admit as much in a response to a reviewer, writing “our contention that LGMR improves upon our model priors is not based on any particular metric of prior vs. posterior ensemble spread, but rather our external validation tests”.
Conclusions
I do not consider Osman 2021’s main LGMR, data-assimilation reconstruction, which estimates 6.8°C mean LGM cooling, to be reliable. It is highly dependent on the spatiotemporal accuracy of LGM simulations by a single GCM. The external validation tests, when analysed properly, show no significant skill by either the model simulation prior or the LGMR posterior in predicting observed LGM changes in independent cave speleothem records. Moreover, those tests show that both the model prior and the LGMR posterior substantially overestimate observed LGM changes per independent ice core records. While the LGMR reconstruction is innovative, I am doubtful that the accuracy of model simulations and the spatial coverage and accuracy of proxy data over the period extending back to the LGM are adequate for a data-assimilation approach to give unbiased GMAT estimates. In my view, the method employed by Annan and Hargreaves (2013)[28], which scales model-simulation cooling patterns to best match proxy data (giving an estimate of 4.0°C LGM cooling in their case), is more suitable.
In my view, Osman 2021’s preprint proxy-only reconstruction appears credible, although a lower SST multiplier than they used is appropriate. I consider it to be more credible than the version of their proxy-only reconstruction published in Nature, as no explanation was given for that being different from the reconstruction in their preprint, and it matches the shape of the de facto preexisting standard SMC reconstruction time series less well than the preprint version. Using a multiplier based on the mean from the most recent, PMIP4 models, estimated average LGM GMAT was ~4.6°C cooler than preindustrial per the preprint proxy-only reconstruction. If, unlike in GCMs, SST actually changes as much as marine air temperature, as assessed by the IPCC in AR6, then the implied GMAT cooling would instead be ~4.3°C.
Addendum
Since writing this article a new Holocene study, Thompson et al. (2022), has been published in Science Advances (open access). Using the same GCM as Osman 2021, it shows that adding forest cover in the Sahara and mid-latitudes (partial at 3 kyr BP) and (except at 3 kyr BP) in the Arctic, to match pollen records substantially increases simulated GMAT at 3, 6 and 9 kyr BP. The difference at 6 kyr BP is 0.72°C, with the resulting GMAT being well above the preindustrial level. Osman 2021’s simulations incorporated this greening only partially.[29] Even with all these regions greened, the model simulation (prior) 6 kyr BP GMAT was still well below that of the Osman 2021 proxy-only reconstruction. These facts suggest that Osman 2021’s model prior may be particularly unsatisfactory, spatially as well in the global mean, during the Holocene.
Nicholas Lewis 25 April 2022
[1] L. Resplandy, R. F. Keeling, Y. Eddebbar, M. K. Brooks, R. Wang, L. Bopp, M. C. Long, J. P. Dunne, W. Koeve & A. Oschlies, 2018: Quantification of ocean heat uptake from changes in atmospheric O2 and CO2 composition. Nature, 563, 105-108. https://doi.org/10.1038/s41586-018-0651-8
[2] Osman, M.B., Tierney, J.E., Zhu, J., Tardif, R., Hakim, G.J., King, J. and Poulsen, C.J., 2021. Globally resolved surface temperatures since the Last Glacial Maximum. Nature, 599(7884), pp.239-244. https://www.nature.com/articles/s41586-021-03984-4 Preprint available at https://eartharxiv.org/repository/object/2219/download/4584/
[3] Tierney, J.E., Zhu, J., King, J., Malevich, S.B., Hakim, G.J. and Poulsen, C.J., 2020. Glacial cooling and climate sensitivity revisited. Nature, 584(7822), pp.569-573. https://www.nature.com/articles/s41586-020-2617-x
[4] GMAT is referred to as GMST in Osman 2021.
[5] Kageyama, M., et al.., 2021. The PMIP4 Last Glacial Maximum experiments: preliminary results and comparison with the PMIP3 simulations. Climate of the Past, 17(3), pp.1065-1089. Note that of the four PMIP4 simulations with a GMAT exceeding 5.3°C, three are by a variants of HadCM3, an old model that dates back three climate model generations, and one is by the base-version model (CESM1-2) of that used by Osman 2021, for which it was subsequently found that the simulated LGM climate is very sensitive to treatments of cloud microphysical processes.
[6] They also estimate cooling of 7.0°C at the point of deglaciation onset, but it is standard to take the mean over a period of several thousand years. Moreover, their only GCM simulations circa the LGM were at 18,000 and 21,000 yr BP
[7] Taking the uncertainty distributions to be normal, the distribution of their difference has only a little over 5% of its probability in the region where the two estimates are compatible.
[8] The estimated relationship between proxy data and local SST together with other relevant climate variables is reflected in ‘forward models’ of proxy values. SST estimates can then be derived using the proxy data and estimates of the other climate variables involved, via Bayesian ‘inverse models’. SST estimates therefore depend on the forward models, on the related Bayesian inverse models, and on the ancillary climate variable estimates used in addition to the SST proxy data. Much of the resulting uncertainty is unavoidable, however the use of Bayesian inverse models introduces a further source of uncertainty and possible bias, in addition to that (including as to age calibration) arising directly from the nature of the proxies.
[9] The 60°S–60°N mean SST to GSAT scaling factor used in the final Nature paper was 1.90, a mean value originally derived from PMIP2 and PMIP3 simulation data.
[10] BP: before present
[11] The 200-yr resolution reconstruction values are all at odd multiples of 100 years BP.
[12] The plotted lines are accurately digitized copies, with the preprint version rescaled from 2.44 to 1.90 times mean 60°S−60°N SST to GMAT to match the 1.90 scaling in the Nature version. The preprint line has also been shifted by −0.25°C to rebase it to match the Nature version (which takes preindustrial from the means of up to the last 4,000, rather than 1,000, years proxy values). Note that the Fig. 4a version in Nature appears to have been stretched slightly in the time dimension and shifted it by 100 years, relative to the published data. The preprint version very likely did the same, since its turning points coincide with those in the Nature version.
[13] The 2.44 mean scaling factor was taken from a study involving a proxy-derived estimate of the change in mean temperature of the ocean interior, not of the change in SST. Bereiter, B., Shackleton, S., Baggenstos, D. et al., 2018. Mean global ocean temperatures during the last glacial transition. Nature 553, 39–44.
[14] One potentially relevant difference is that only the Nature version mentions including data from those proxies for which an estimate of preindustrial temperature could not be derived from core-top values, with instrumental reconstruction values being used instead. It is not obvious why that should lead to a larger LGM to preindustrial temperature change in the Nature version, but it is possible since SST estimates from the affected proxies might generally be negatively biased and/or the .instrumental reconstruction values might have positive biases.
[15] This is after increasing the warning from the 19,000–22,000 yr BP period, which the proxy-only reconstruction does not extend beyond, by the 0.015°C by which Osman 2021’s LGMR 19,000-23,000 yr BP mean GMAT was cooler than its 19,000-22,000 yr BP mean. Mean PI temperature is almost the same whether the mean of the last 600, 400 or 200 years is used. Note that the mean scaling factors used in the Nature version of Osman 2021 have been used, with uncertainty in them, and other uncertainties, being ignored.
[16] Snyder, C.W., 2016. Evolution of global temperature over the past two million years. Nature, 538(7624), pp.226-228. https://climate.fas.harvard.edu/files/climate/files/snyder_2016.pdf
[17] Friedrich, T., Timmermann, A., Tigchelaar, M., Elison Timm, O. and Ganopolski, A., 2016. Nonlinear climate sensitivity and its implications for future greenhouse warming. Science Advances, 2(11), p.e1501923.
[18] Using the more recent PMIP4 data, from simulations by much more advanced models and incorporating updated ice-sheet etc. boundary conditions I derive a mean scaling factor of 1.64 from 60°S–60°N ocean surface air temperature to GSAT. (Kageyama et al, 2021.The PMIP4 Last Glacial Maximum experiments- preliminary results and comparison with the PMIP3 simulations, Clim.Past, https://doi.org/10.5194/cp-17-1065-2021) Kageyama et al, 2021 does not give values for SST.
[19] Although in GCMs ocean surface air temperature changes more than SST, the IPCC AR6 report concluded that evidence for this, either from theory or observations, was poor, and that GCM behaviour might reflect a common model bias arising from use of the same parameterization. AR6 therefore assessed, as its best estimate, no difference between SST and ocean surface air temperature changes.
[20] Since there are 2 or 3 kyr gaps between the GCM simulations it is difficult to see that the true time resolution of the reconstruction can be anywhere near as good as 200 years.
[21] Previously developed code packages that implement the Kalman filter and the proxy forward models have been made publicly available, but not the code that Osman 2021 developed to produce their reconstructions using those packages, nor the model simulation data that they used. This makes replicating their results and evaluating the effect of varying their assumptions exceedingly difficult if not impossible.
[22] It is not completely clear to me from the Methods descriptions in Osman 2021 and Tierney 2020 how exactly the model priors and covariances were calculated, or the down-weighting applied, but that is not directly relevant to the issues raised here. Note that to limit spurious relationships between proxies and far away regions, a localization weighting was applied that downweights covariances between far distant points, with strong downweighting where their separation exceeds ~10,000 km.
[23] iCESM1.2 is a water isotope-enabled variant of the main CESM1.2 model. For two simulations, Osman 2021 used the similar iCESM1.3 variant in addition to iCESM1.2.
[24] The former range is much closer to the value of 14.2°C for CESM1.1 per Figure 1 of Bacmeister et al., 2020. CO2 Increase Experiments Using the CESM: Relationship to Climate Sensitivity and Comparison of CESM1 to CESM2. JAMES12, e2020MS002120. https://doi.org/10.1029/2020MS002120
[25] If one combines two sets of paired (x,y) values, each with zero correlation between its x and y values, but the two sets have different mean x and y values, the x and y values of the merged data set will be correlated.
[26] 21 kyr BP is the mid-point of the stable 19-23 kyr BP period usually taken as representing the LGM.
[27] Regression forced through the origin gives a similar value for LGMR posterior overestimation of LGM cooling.
[28] Annan, J.D. and Hargreaves, J.C., 2015. A perspective on model-data surface temperature comparison at the Last Glacial Maximum. Quaternary Science Reviews, 107, pp.1-10. https://dx.doi.org/10.1016/j.quascirev.2014.09.019
[29] None of Osman 2021’s 3kyr BP simulations partially greened the Sahara and northern hemisphere mid-latitudes. Only two thirds of their 6 kyr BP simulations greened the Sahara and the Arctic (north of 50°N); none greened mid-latitudes. None of their 9 kyr BP simulations greened either the Arctic or mid-latitudes. Moreover, their 6 kyr BP simulations that did green the Sahara and Arctic had a mid-range GMAT only 0.27°C warmer than those that didn’t do so, whereas per Thompson et al. in such simulations the average difference was 0.57°C.
Leave A Comment