A pdf copy of this article is available here. Originally a guest post 5 September 2018 at Climate Etc.
Plain language summary
- A new paper led by a UK Met Office scientist claims that accounting for the difference in the spatial pattern of surface temperature change between that in the historical period and that projected under long-term CO2-forcing substantially increases historical estimates of climate sensitivity. The claims are based on simulations by global climate models (GCMs) from the UK Met Office and three other institutions, driven by historical (last ~150 years) observations of sea-surface temperature (SST) and sea-ice.
- The simulations show that the models’ effective climate sensitivity is substantially lower when driven by an observationally-based estimate of the evolution of SST and sea-ice over the historical period than when responding to long-term CO2 forcing. This finding underlies the authors’ conclusion that climate sensitivity estimates based on observed historical warming are too low.
- The sensitivity of the results to the data used was tested by repeating the simulations by the two UK Met Office GCMs using a more recent SST and sea-ice dataset – an updated and improved version of the dataset that provided the sea-ice data used in the original simulations. The results, which appeared in the paper’s Supporting Information but were not reported in the paper itself, were completely different.
- The divergence between the simulation results presented in the paper itself and in its Supporting Information show that the authors’ key claim, that climate sensitivity estimates based on observed historical warming are too low, are highly sensitive to the SST and sea-ice dataset used. Results using the more recent dataset contradict their claims, largely due to differences between the two datasets in the evolution of sea-ice more than counteracting the effects of evolving patterns of SST change over the open ocean. I therefore think it is difficult to draw any strong conclusions from the simulation results presented in the paper.
- Moreover, the study conflates two different temperature-change pattern effects, both of which affect estimated climate sensitivity in GCMs:
- that arising from the difference between the simulated spatial pattern in response to long-term CO2-forcing and the spatial pattern simulated when GCMs respond autonomously to evolving forcing over the historical period; and
- that arising from the difference between the spatial pattern over the historical period simulated when GCMs respond autonomously to evolving forcing and the spatial pattern when they are driven instead by a specified, observationally-based, evolution of SST and sea-ice, with unchanging forcing.
- The first pattern effect concerns forced changes and has been shown to lead to modest (~10%) underestimation of estimated equilibrium climate sensitivity (ECS) for typical current generation GCMs (range -10% to + 50%)[1], although two published studies incorrectly claimed that the effect was much larger.
- The second pattern effect is only relevant to observational estimation of climate sensitivity to the extent that it is caused by natural climate system internal variability. That extent cannot be major – contrary to what the new paper implies – if current GCMs realistically simulate climate system internal variability. All or part of the second pattern effect might instead be attributable to GCMs incorrectly representing historical forcing and/or the climate system’s response thereto, and/or to inaccuracies in the observational SST and sea-ice dataset used.
Introduction
Soundly-derived recent estimates of effective climate sensitivity (EffCS)[2] based on observed warming over the historical period, EffCShist, have generally been in the 1.6–2.0°C range. That is well below EffCShist estimates for general circulation models (GCMs, also called global climate models) driven by historical forcing, which for current generation (CMIP5) models average 3.0°C (Lewis and Curry 2018).[3] Those estimates are for GCMs with their atmospheric model coupled to a 3D dynamic ocean model (AOGCMs).
A new paper (Andrewsetal18)[4] compares “amipPiForcing” simulations by six AGCMs (the atmospheric model components of AOGCMs) with CO2-forced simulations by their corresponding AOGCMs.[5] Two of the AGCMs used were developed at the UK Met Office – where the lead author works – and the remainder at three other modelling centres. Almost all the simulation results have been published previously; this paper brings them together and makes comparisons.
The new paper is titled “Accounting for changing temperature patterns increases historical estimates of climate sensitivity”. I consider that statement to be unjustified in the light of the simulation results reported by the authors. In order to show why, I need to go in some detail into pattern effects and what the paper shows about them. The term “pattern effect” refers to the effect on radiative feedback, and on climate sensitivity estimates derived therefrom, of the spatial pattern of evolving surface temperature change. Pattern effects can in general only be estimated in GCMs. In Andrewsetal18, the focus is on the effect on estimated climate sensitivity in GCMs of the difference between the spatial pattern of observed changes over the historical period and that which they project to occur under long-term CO2-forcing.
The types of simulation and related measures of climate feedback and sensitivity involved
In amipPiForcing simulations (a type of amip simulation)[6], AGCMs are driven by the observed historical (1871-2010) evolution of sea-surface-temperature (SST) and sea-ice, rather than by changing radiative forcing. Since land temperatures are mainly determined by SST, these AGCM simulations involve a similar surface temperature pattern evolution and trend to that of historical climate change observations, notwithstanding that atmospheric composition is set at its preindustrial level throughout,[7] which implies unchanging radiative forcing.
Although Andrewsetal18 refer to the effect of the pattern of observed historical SST change, the GCM simulations that they employ are driven by combined SST and sea-ice changes, as is standard for amip simulations. Variation in sea-ice is an important element as it strongly affects local surface temperature and albedo, as well as having remote effects. I treat temperature change pattern effects as including the part of the simulation results attributable to sea-ice changes as well as that attributable to changes in open ocean SST; this is in my view the natural interpretation since the simulations results presented in the paper reflect the strength of the combined SST and sea-ice changes.
The paper compares climate feedback[8] (λ) over the amipPiForcing simulations (λamip) with feedback over similar length abrupt4⤬CO2 simulations, in which CO2 concentration is initially quadrupled and then held steady (λ4⤬CO2). The authors find that in the amipPiForcing simulations, feedback is robustly more stabilizing (stronger) than in abrupt4xCO2 simulations. Since effective climate sensitivity is reciprocally related to feedback strength (|λ|), the related amipPiForcing EffCS estimates, EffCSamip, are smaller than those derived from the abrupt4xCO2 simulations, EffCS4⤬CO2.
In the abstract to Andrewsetal18, EffCS is used to refer to effective climate sensitivity as derived from warming and radiative changes over the historical period (EffCShist), while in section 2 of the paper EffCS is used to refer to that estimated from regression over years 1-150 of abrupt4⤬CO2 simulations (EffCS4⤬CO2), which the authors use as a proxy for long-term climate sensitivity. Comparing, as Andrewsetal18 do, EffCSamip with EffCS4⤬CO2 rather than with EffCShist conflates two conceptually distinct pattern effect issues.
The first issue concerns the effect in GCMs on feedback strength, and hence on EffCS, of the difference between the simulated spatial pattern of temperature change in response to long-term CO2-forcing and that simulated in response to evolving forcing over the historical period. There is no good evidence that this pattern effect is reduced if the evolving composite forcing during the historical period is replaced by smoothly increasing CO2-only forcing.[9] Rather, this pattern effect is dominantly related to the time elapsed since forcing was applied. This time-dependent pattern effect is relevant to estimation of the difference in AOGCMs between EffCShist and true equilibrium climate sensitivity (ECS), as approximated by EffCS4⤬CO2 or otherwise. Observed warming plays no role in it.
The second pattern effect issue concerns the effects on EffCS estimates in GCMs of differences between model-simulated forced warming patterns and observed warming patterns over the historical period (from the third quarter of the 19th century until recent years). That is reflected in the difference between EffCSamip and EffCShist. It may be relevant to comparing estimates of ECShist based on observations and on forced GCM historical simulations. Since historical forcing was not generally diagnosed in CMIP5 models (and evidently differs considerably between them), their responses to comparable duration CO2-only forcing are typically used to estimate their ECShist.
As it is not central to my main criticism of Andrewsetal18, discussion of differences between ECShist and long-term climate sensitivity estimates in AOGCMs appears in an appendix (Appendix A). However, in order to provide more relevant comparatives, I include λhist and ECShist estimates in Tables 1 and 2 in addition to the EffCS4⤬CO2 values given by Andrewsetal18. The λhist and ECShist estimates are derived from regression over the first 50 years of abrupt4xCO2 simulations, which provides satisfactory values for them[10] and can be calculated for all six AOGCMs.
Effect on EffCS in GCMs of differences between observed and simulated historical warming patterns
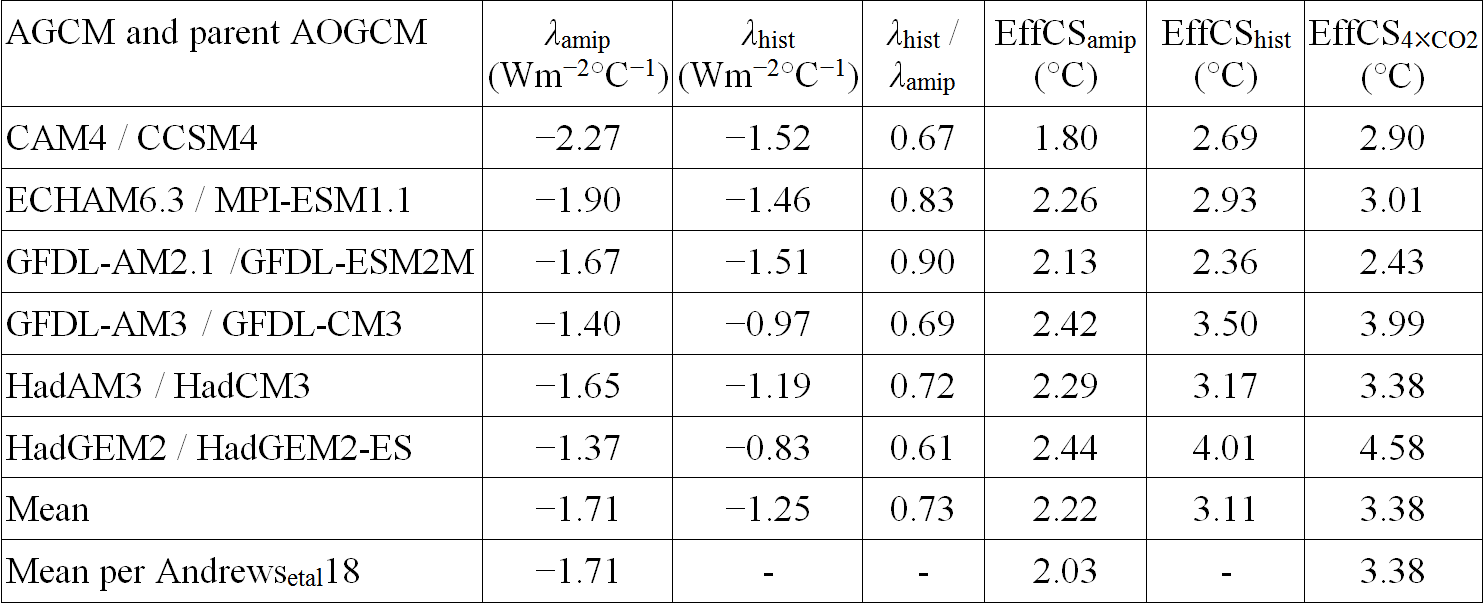
Andrewsetal18 examines estimates of the climate feedback parameter λamip[11] operating over 1871-2010 in amipPiForcing simulations by eight AGCMs,[12] each driven by the AMIP II observationally based SST and sea-ice dataset. They estimate λ as the slope of an ordinary least-squares (OLS) linear regression fit (with intercept) of planetary radiative imbalance (N) on global surface temperature (T), using annual mean data, as is common.[13] They compare λamip with λ4⤬CO2, the latter reflecting the OLS regression fit over years 1-150 of the abrupt4xCO2 simulation. Their long-term climate sensitivity estimate, EffCS4⤬CO2, is derived from the same regression line, by halving its x-intercept.[14] They compare EffCS4⤬CO2 with EffCSamip, derived as EffCSamip = F2⤬CO2 / |λamip|), F2⤬CO2 being an estimate of the forcing from a doubling of preindustrial CO2 concentration. This derivation is valid provided that the F2⤬CO2 estimate represents an effective radiative forcing (ERF).[15] For the six models where comparison was possible, they find that feedback strength is much higher in the amipPiForcing simulations, resulting in a climate sensitivity estimate that – based on the F2⤬CO2 values they use to convert λamip to EffCSamip – is on average 40% lower than their long-term value.
However, Andrewsetal18’s EffCSamip value is reached by dividing |λamip| into an estimate of F2⤬CO2 derived from regression over years 1-150 of abrupt4xCO2 simulations. Such an estimate of F2⤬CO2 does not correspond to the ERF involved where, as is normally the case, λ changes over years 1-150 of the abrupt4xCO2 simulation; indeed, is has no physical interpretation (see Box 1). Accordingly, EffCSamip values should not be derived using such F2⤬CO2 estimates. I show corrected EffCSamip values that use F2⤬CO2 estimates derived from regression over years 1-50 of abrupt4xCO2 simulations, which are little affected by changes in λ. That F2⤬CO2 estimate is a good measure of ERF,[16] and on average agrees with the F2⤬CO2 estimate from a model that uses accurate radiation codes.[17] Using the estimate of F2⤬CO2 derived from regressing over years 1-50 of each GCM’s abrupt4xCO2 simulation to convert its λamip estimate to a corresponding EffCSamip value is therefore an appropriate choice. That F2⤬CO2 value is moreover the one implicit in the relation between our estimates of λhist and EffCShist.
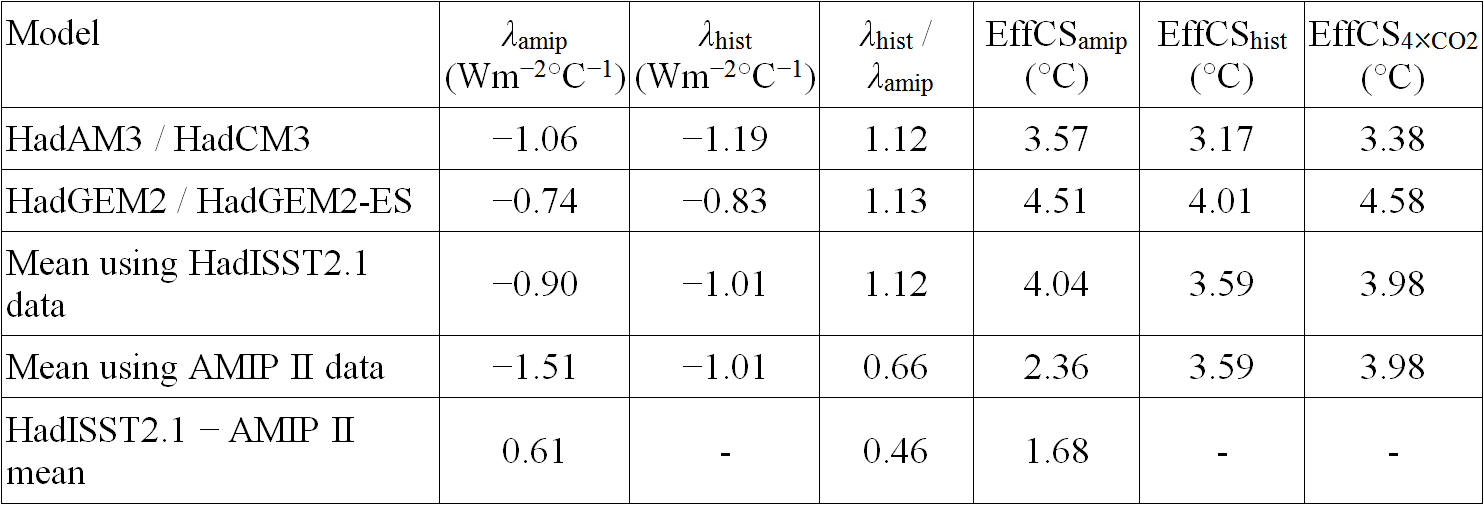
Table 1 is a version of Andrewsetal18 Table 1, with the corrected EffCSamip values referred to above, that includes the six models for which all the necessary data is available; CAM5.3 and GFDL-AM4 are omitted since no estimates of any EffCS values were given for those models. The resulting mean EffCSamip value is 34% below the (unchanged) mean EffCS4⤬CO2. Since the Andrewsetal18 λ4xCO2 values can only be converted to a climate sensitivity using an unphysical F2⤬CO2 value, I have replaced them with λhist, estimated as stated above, which is in any event a more appropriate comparative for λamip.
Table 1. Results from simulations driven by AMIP II SST/sea-ice versus those driven by CO2 forcing
It is clear from Table 1 that, even when comparing λamip with an estimate of λ corresponding to that derivable from historical period information (λhist), all six models show a noticeably stronger climate feedback (λamip ) – and hence a correspondingly lower EffCS (EffCSamip) – over the historical period when driven by observationally-based SST and sea-ice evolution than when allowed to generate their own SST and sea-ice patterns in response to radiative forcing (λhist and EffCShist). Their estimated long-term climate sensitivities (EffCS4⤬CO2) are higher still, but on average they exceed EffCShist by only 8%.
Do the amipPiForcing simulations justify the key claim in Andrewsetal18?
Andrewsetal18 claim in their title that accounting for changing temperature patterns increases historical estimates of climate sensitivity. Elaborating on this, in the final section of the paper it states “The pattern effect causing the difference between EffCS under historical climate change and long-term CO2 changes implies that current constraints on climate sensitivity that do not consider this give values that are too low…”. The wording is unconditional in both cases. Such an unqualified claim is unjustified. To justify such a claim one would need, at least, to establish:
- that correctly-calculated EffCSamip estimates are adequately robust to choice of historical SST and sea-ice observational dataset;
- that the differences between λamip and λhist could feasibly be due to natural internal climate system variability; and
- that the long-term SST and sea-ice patterns simulated by AOGCMs, and the radiative response to them are realistic.
In the paper’s Abstract, the key claim made in the paper is qualified as dependent on the assumption that point 3 is true. However, in its title and its final section no such qualification is made. Points 1 and 2 are elaborated upon in the following sections.
1: Non-robustness to the observational SST and sea-ice dataset used
Observational estimates of patterns of SST and sea-ice are inevitably more uncertain, particularly during the first half of the historical period, than estimates of global mean surface temperature, which are all that historical period energy budget based climate sensitivity estimation requires. The AMIP II SST and sea ice dataset used for the amipPiForcing simulations analysed in the paper was developed some time ago; for sea ice it essentially reflects HadISST1, a dataset originally released in 2003. In 2014 the sea ice component of an improved dataset, HadISST2.1, that used new data sources that had become available and applied bias adjustments, was released,[18] followed more recently by the SST component. Therefore, the sensitivity of the results to a change of SST and sea-ice dataset can be tested.
Andrewsetal18 very appropriately investigated, in their Supporting Information, whether the amipPiForcing results were robust to different datasets by carrying out further simulations with the two UK Met Office models, HadGEM2 and HadAM3, using the more recent, improved, HadISST2.1 dataset. Using Andrewsetal18’s 30-year sliding window regression method, variation in feedback strength in HadGEM2 spans a similar range when driven by HadISST2.1 SST and sea-ice as when driven by the older AMIP II datasets that uses HadISST1 sea-ice (Figure 1).[19]
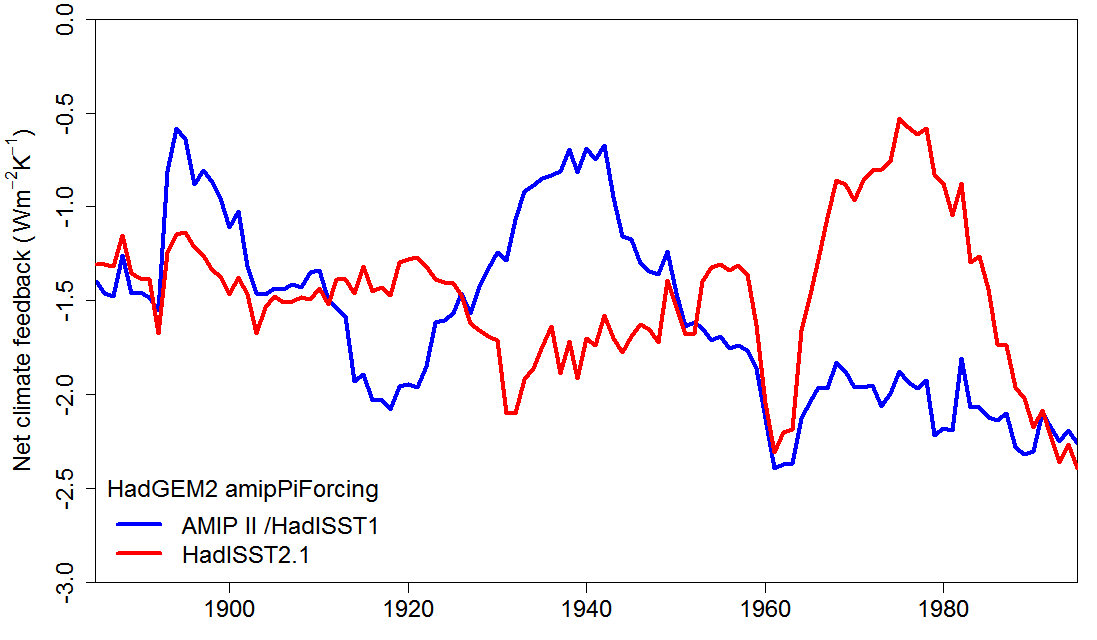
However, regression analysis using a 30-year sliding window gives a misleading impression of feedback in HadGEM2 over the full period. Feedback over 1871-2010 nearly halves upon switching SST and sea-ice dataset from AMIP II to the newer HadISST2.1.
Table 2 gives full period results on the same basis as for Table 1, with results from that table shown for comparison. The mean EffCSamip for the two Hadley models is 71% higher when using the new rather than the old dataset to drive the amipPiForcing simulations – it is 13% higher than EffCShist,[20] as opposed to 34% lower when using the old dataset. EffCSamip even exceeds the long-term sensitivity, EffCS4xCO2. Moreover, based on regression using pentadal rather than annual means, which is generally more reliable, for HadGEM2 (I do not have HadAM3 data) EffCSamip is 5.11°C, 13% higher still and 28% above its EffCShist.[21]
Table 2. Results from Hadley model amipPiForcing simulations driven by HadISST2.1 SST and sea-ice data. Means are for HadGEM2 and HadAM3 only. As in Table 1, for each model EffCSamip and EffCShist are both calculated using the appropriate common F2⤬CO2 estimate, derived from regressing over years 1-50 of their abrupt4xCO2 simulation.
There is no hint of these remarkable results in the paper itself. The main text merely comments that “The sensitivity of the results to the AMIP II boundary condition dataset is explored with analogous experiments using the HadISST2.1 SST and sea-ice dataset”. But, as can be seen, results using the HadISST2.1 dataset are radically different from those based on the AMIP II dataset – the sole dataset used throughout the paper itself.
Using AMIP II data, climate feedback was much stronger (more negative) in amipPiForcing simulations than in forced simulations where the models simulated their own SST and sea-ice patterns in response to long term CO2 forcing or (less markedly) to historical forcing.[22] Using HadISST2.1 SST and sea-ice data, the opposite result was obtained.
If the same mean 1.71 ratio of HadISST2.1 based EffCSamip to AMIP II based EffCSamip found in the Hadley models applied to all six models in Table 1, the mean EffCSamip would be 22% higher than EffCShist rather than 28% lower, and would also exceed the mean EffCS4xCO2 by 12%.
In my opinion the ancillary HadISST2.1-based results contradict the strong claims made in the paper. While it could be that the HadISST2.1 dataset is actually less realistic than the older AMIP II dataset, the large difference in results using the two datasets shows that the EffCSamip estimates are highly sensitive to the SST and sea-ice dataset used.
The bulk of the difference in λamip arising when the HadISST2.1dataset is substituted for the AMIP II dataset is caused by differences in their sea-ice data, primarily in the Southern Hemisphere. Andrewsetal18 quantify the sea-ice contribution in HadAM3, at 71%, and imply that it is 100% in HadGEM2.[23] Appendix B examines the differences in the evolution of sea-ice in the two datasets. In their Supporting Information, Andrewsetal18 discuss analysing the HadISST2.1 based amipPiForcing simulation data over sub-periods that exclude the 1970s decade, over which the difference between their Antarctic sea-ice fraction largely arose. They find, unsurprisingly, that when they do so climate feedback in amipPiForcing simulations is much less affected by which SST and sea-ice dataset is used. But that is irrelevant. The fact is that their main results are completely non-robust to the use of a different, indeed newer, SST and sea-ice dataset. Since most of the difference in feedback arises from different changes in Antarctic sea-ice, it is unsurprising that the differences in feedback would be much smaller if the analysis was restricted to sub-periods over which the two datasets displayed similar changes in Antarctic sea-ice.
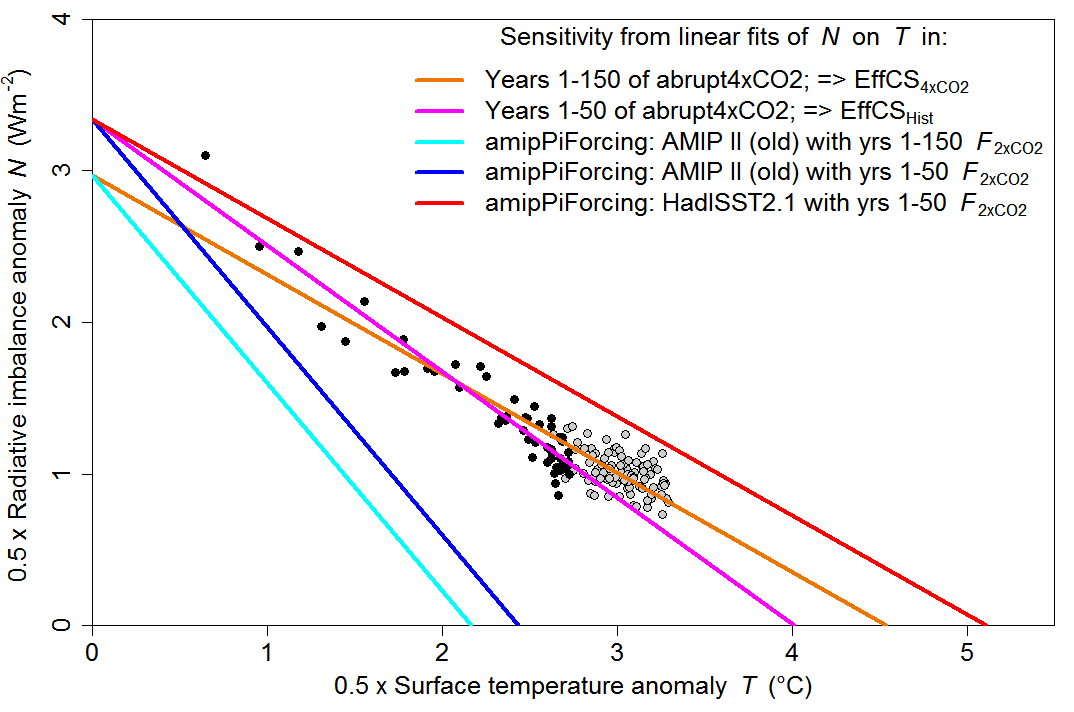
Box 1: A graphical illustration of the derivation of the various EffCS estimates
The amipPiForcing results that Andrewsetal18 obtained using HadGEM2A, and results from the coupled HadGEM2-ES abrupt4⤬CO2 simulation, are illustrated in Figure 2. OLS regression of the annual, global mean top-of-atmosphere radiative imbalance anomaly[24] on surface temperature over years 1-50 of the abrupt4⤬CO2 simulation (filled black circles; magenta line) provides a physically-reasonable estimate of F2⤬CO2 in this model, at 3.34 Wm−2. That estimate is the same as when regressing over years 2-10, recommended in Lewis and Curry (2018), and slightly below the 3.5 Wm−2 estimate derived from fixed-SST simulations.[25] The x-intercept from regression over years 1-50 provides the EffCShist estimate of 4.01°C. Dividing |λamip| based on the old AMIP II dataset into that F2⤬CO2 estimate (blue line x-intercept) gives an EffCSamip estimate of 2.44°C, while λamip based on the new HadISST2.1 dataset gives an EffCSamip estimate of 4.51°C (solid green line), or 5.11°C if pentadal rather than annual mean amipPiForcing data is regressed (dotted green line).
Regression over years 1-150 of the abrupt4⤬CO2 simulation (black and grey filled circles; orange line) gives a long-term climate sensitivity estimate, EffCS4xCO2, of 4.58°C. The corresponding F2⤬CO2 estimate, of ~2.95 Wm−2 is depressed by climate feedback in HadGEM2’s abrupt4xCO2 simulation weakening after the first few decades and is not physically-meaningful; it does not correspond to the effective radiative forcing from a doubling of CO2 concentration. The AMIP II dataset based EffCSamip value of 2.14°C that Andrewsetal18 calculate by dividing | λamip| into that F2⤬CO2 value (cyan line x-intercept) is accordingly artificially low.
2: Differences between λamip and λhist are inconsistent with CMIP5 models’ internal variability
My second reason for disputing the strong, GCM-based, conclusions of Andrewsetal18 is that the differences between their estimates of λamip and λhist are too large to be accounted for by natural internal climate system variability as simulated by CMIP5 models. Lewis & Curry (2018) showed, for the HadGEM2 model amipPiForcing results given in Gregory and Andrews (2016) [26], that if internal climate variability simulated by CMIP5 models was realistic, such variability was exceedingly unlikely to account for more than a small part of the difference in feedback strength between the HadGEM2 amipPiForcing and abrupt4xCO2 simulations. The same is true for five of the six GCMs listed in Table 1. Only for GFDL-AM2.1 could internal variability simulated by CMIP5 AOGCMs account for the difference between the Table 1 λamip and λhist values in more than a tiny fraction of cases. GFDL-AM2.1 has the highest λhist / λamip ratio (0.90) of the six models. For the other five models, internal climate system variability can be ruled out as the cause of the difference between λamip and λhist in all but 0.2% of the almost 92,000 cases tested.[27] It is possible that internal variability in CMIP5 AOGCMs may be unrealistic. However, if it is unrealistic, then is it reasonable to rely on the forced warming patterns that CMIP5 AOGCMs generate being correct?
Conclusions
IMO, the strong claims made by Andrewsetal18 are unjustified. Their claims are dependent, inter alia, on the accuracy of the AMIP II observational SST and sea-ice dataset employed, the sea-ice data part of which comes from HadISST1. However, when the newer HadISSST2.1 version of the HadISST1 dataset is used in place of the AMIP II dataset in amipPiForcing simulations by the two Hadley models, the relationships in them between the effective climate sensitivity implied by the amipPiForcing simulations and CO2-forced EffCS – both that corresponding to the historical period and the long term measure – is reversed. It is not known which dataset is more realistic.
Andrewsetal18 seek, unconvincingly, to discredit the HadISSST2.1 based full-period amipPiForcing simulation results, which I view as casting strong doubt on key claims in their paper. Justifying the exclusion of 1970s data on the basis that it does not well-fit their regression analysis, they restrict that analysis to two sub-periods over which the sea-ice trends in the HadISSST2.1 and HadISSST1 datasets are almost identical. However, over the full 1871-2010 period the HadISSST2.1 Antarctic sea-ice fraction trend is three times that in HadISSST1, whether or not 1970s data are excluded.
The contrasting simulation results discussed in Andrewsetal18 and its Supporting Information show that whether climate feedback strength in amipPiForcing simulations is greater over the historical period than in long-term CO2-forced simulations depends on the SST and sea-ice dataset used; results using the more recent, improved, dataset suggest not. It follows that the Andrewsetal18 conclusion that accounting for changing temperature patterns increases historical estimates of climate sensitivity cannot be satisfactorily reached from their results. Moreover, the amipPiForcing results in the paper itself are inconsistent with internal climate system variability as simulated by CMIP5 models.
Appendix A: Differences between ECShist and ECS estimates in AOGCMs
In most cases the forcing data required to estimate ECShist from AOGCM historical simulations are unavailable, so their responses during appropriate periods of simulations involving CO2 concentration increasing at 1% per annum compound (1pctCO2) and/or abrupt4⤬CO2 simulations are used instead.[28] Andrewsetal18 notes that the use of 1pctCO2 simulations as an analogue for historical climate change has important limitations in that it neglects the impact from non-CO2 forcings and unforced climate variability that could have had a significant impact on the pattern of historical temperature change. However, AOGCM warming patterns are typically similar in 1pctCO2 simulations, in the early decades of abrupt4xCO2 simulation cases and in historical simulations, and there is no evidence of systematic differences in AOGCM ECShist estimates derived from the three types of simulation.[29]
Since most AOGCMs have not been run to equilibrium at an increased CO2 level, recent papers have estimated AOGCM ECS values from their abrupt4xCO2 simulations (which are normally 150 years long) either by regression over years 21–150 (e.g., Armour 2017)[30] or by fitting a two or three time constant exponential model to all years (e.g., Geoffroy et al. 2013; Proistosescu and Huybers 2017)[31] [32], which produces similar ECS estimates. In most CMIP5 AOGCMs, doing so results in a higher estimated long-term climate sensitivity than (as in Andrewsetal18) regressing over years 1–150, on average by 6%,[33] but the estimate may nevertheless be lower or higher than the model’s true ECS.[34]
The issue of the relationship of ECShist to ECS in AOGCMs has been investigated in several papers. Armour 2017 and Proistosescu and Huybers 2017 estimated mean ECS-to-ECShist ratios of respectively 1.26 and 1.34 for different ensembles of CMIP5 models. Lewis and Curry (2018) showed that both those papers had methodological biases, and that when these were corrected their median ECS-to-ECShist ratio estimates became closely consistent with those estimated by Lewis and Curry, which gave a median ratio of 1.095 for a larger ensemble of CMIP5 models (range 0.91 to 1.52).[35] That estimate is almost identical to the estimate in Mauritsen and Pincus (2017)[36], which used data from Geoffroy et al. 2013. For the measure of long-term CO2-forced climate sensitivity (ECS) used by Andrewsetal18, the median ECS-to-ECShist ratio in the same set of 31 CMIP5 AOGCMs is only 1.05.[37]
For the new MPI AOGCM, it is possible to closely compare feedback strength arising from historical period forcing and that in long-term doubled CO2 forced simulations in an ensemble of 100 historical period (1850-2005) simulations have been carried out using the MPI-ESM1.1 version, since the evolution of effective radiative forcing (ERF) during them was diagnosed, and a 1000 year simulation to near equilibrium under abruptly doubled CO2 concentration has been undertaken by the nearly identical MPI-ESM1.2 version. Feedback estimates from the MPI-ESM1.2 doubled CO2 simulation should apply also to MPI-ESM1.1; results from years 1-1000 of abrupt4xCO2 simulations by the two model versions are almost identical.[38] From the mean changes in the Earth’s surface temperature and radiative imbalance (from preindustrial levels) in the final century of its doubled CO2 simulation, long term feedback in the MPI-ESM1.2 model is estimated to be in the range −1.32 to −1.35 Wm−2°C−1. These two values use alternative estimates of 3.9 and 4.0 Wm−2 for the level in this model of F2⤬CO2. For either value, the resulting estimate of long term ECS is 2.96 °C. The ensemble-median feedback in MPI-ESM1.1 over the historical period is estimated to lie in the same −1.32 to −1.35 range, depending on estimation method,[39] with ECShist being very marginally lower or higher than 2.96°C according to which of the two F2⤬CO2 estimates is used. So, in this model, ECShist estimated from its historical simulations appears to be almost identical to its long term CO2 forced ECS.
A direct comparison is also possible for the GISS-E2-R model between ECShist estimated from its historical simulations and long term CO2 forced ECS. With the latter derived from regression over years 21–150 of its 150-year abrupt4xCO2 simulation, the model’s ECShist is ~5% below its long term ECS.[40]
Much of any excess of ECS over EffCShist would take centuries to be realised in surface warming. Mauritsen and Pincus (2017) found that warming in 2100 due to the past increase in forcing would be barely affected if ECS exceeded EffCShist in the real world to the same extent as it does in CMIP5 models. So this issue, while of theoretical interest, has little practical relevance over centennial timescales.
Appendix B: Differences between sea-ice evolution in AMIP II and HadISST2.1
As Andrewsetal18 state, sea ice in the AMIP II dataset is essentially that in HadISST1. Figure 3, a reproduction of Andrewsetal18 Figures S1(c) and S1(d), shows the differences in HadISST1 and HadISST2.1 sea ice fraction in respectively the northern and southern hemispheres (NH and SH). The big difference is in Antarctic sea-ice, with much larger reductions compared to preindustrial in HadISST2.1. Both datasets are climatology prior to ~1940 (~1900 for Arctic sea ice), when no observational data is available.
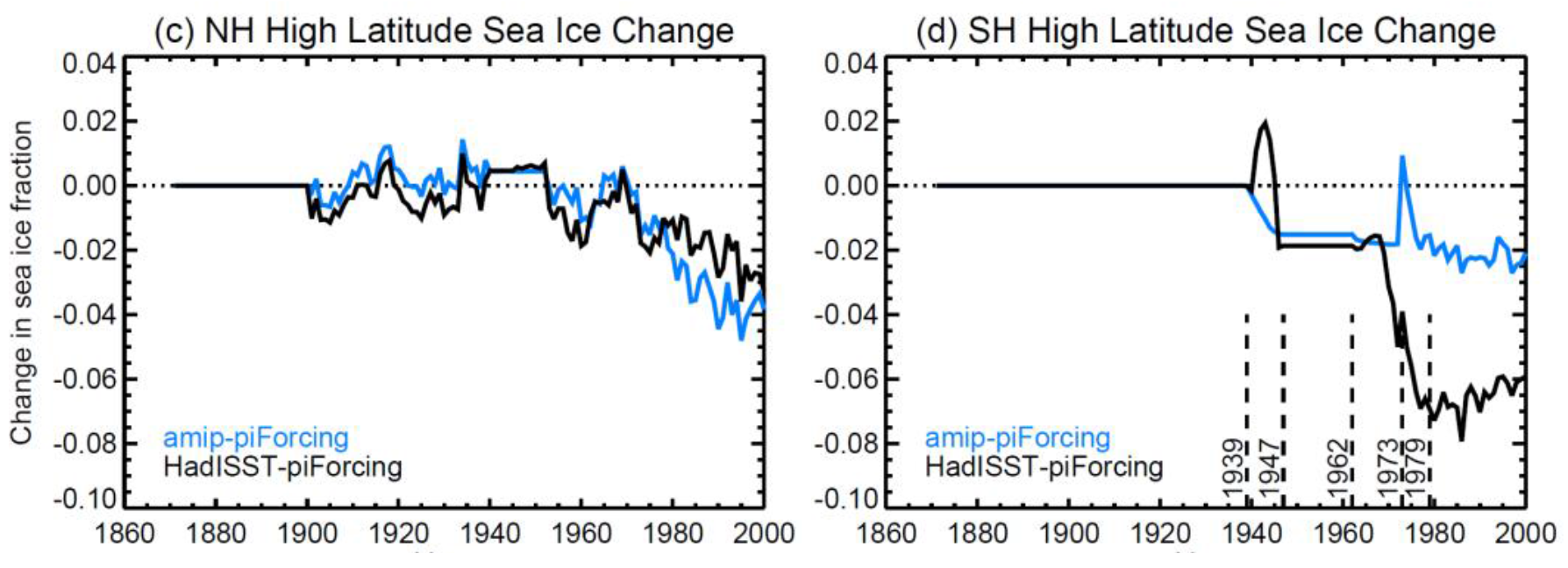
Andrewsetal18 point out that the relationship between temperature and sea ice/radiation is particularly unusual in the HadISST2.1-driven simulations during the 1970s, when sea-ice chart (1973) and passive microwave retrieval (1979) data becomes available. They state that when excluding this period the feedback between amipPiForcing simulations driven by the AMIP II dataset and those driven by the HadISST2.1 dataset becomes much more similar. Simply omitting 1970s data, even if justified, has a negligible effect on feedback in the HadISST2.1 driven HadGEM2 simulations.[41] However, by excluding the 1970s decade, Andrewsetal18 actually mean regressing over the sub-periods 1871–1969 and 1980-2010. Regressing over those sub-periods separately is very different from excluding 1970s data when analysing changes over 1871-2010. Analysing the two periods separately results in the large HadISST2.1 change in Antarctic sea-ice during the 1970s being treated as not existing. Over the full 1871-2010 period, the linear trend in high-latitude SH sea-ice is 3⤬ as high in HadISST2.1 as in HadISST1: −1.5 as against −0.5 % century−1 (of the area poleward of 45°). Simply excluding the 1970s weakens the HadISST2.1 trend by only 4%, and it remains 3⤬ as strong as the equivalent HadISST1 trend.[42]
By contrast, over 1871-1969 the SH sea-ice fraction trends in the old and new dataset are identical, at −0.5 % century−1. They are also identical to each other over 1980–2010, at +1.1 % century−1. So Andrewsetal18’s method of analysis with 1970s data “excluded” in effect makes the HadISST2.1 Antarctic sea-ice record identical to the HadISST-derived AMIP II record, so far as linear trends (which is what Andrewsetal18 use) are concerned. In no way does such an analysis “check whether the amipPiForcing simulation results are robust to different historical SST and sea-ice datasets”, as Andrewsetal18 claim they do.
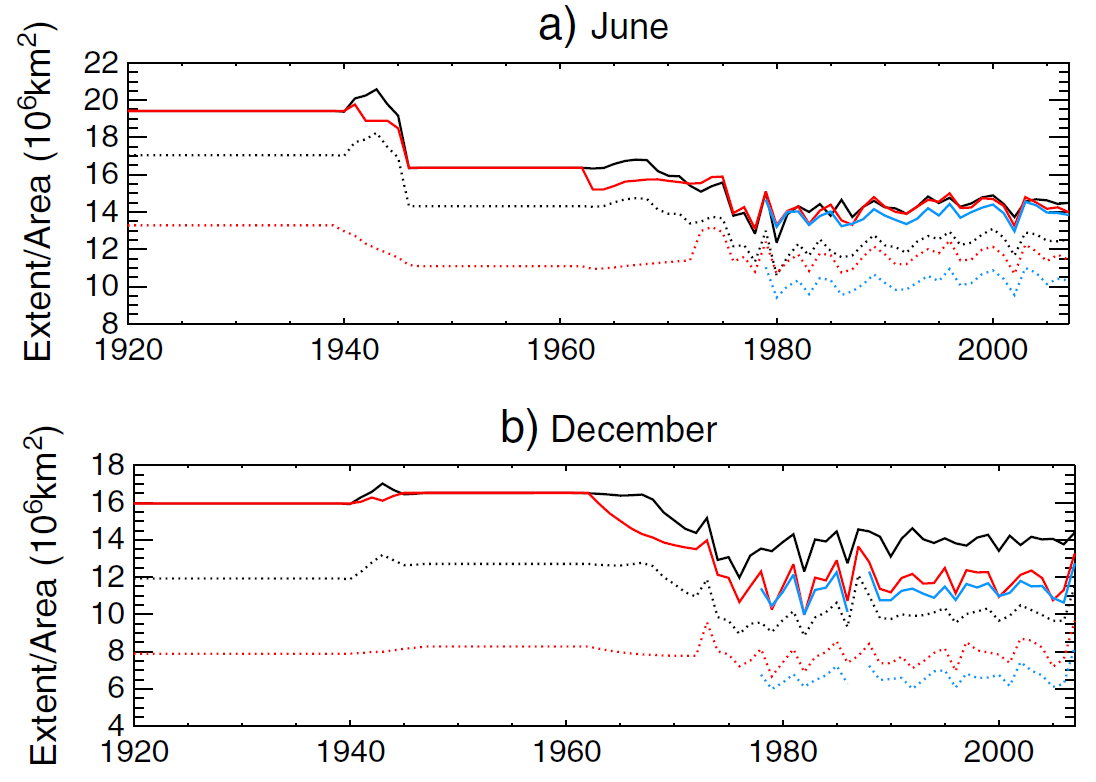
The discussion in Andrewsetal18 also obscures the fact that HadISST2.1 is a newer, improved, version of HadISST1 that uses new data sources that had become available and applies bias corrections. Figure 4, a reproduction of Figure 14 in the paper explaining HadISST2.1 sea-ice concentrations,[43] shows SH June and December sea-ice extent and area; fraction is proportional to area. Values prior to 1920, when there was no observational data, are the same as those in the 1920s. Prior to the early 1970s, sea-ice area is estimated from sea-ice extent (which is taken to be where its concentration is 15%). Over the entire period, sea-ice extent decreases more in HadISST1.1 than in HadISST2.1. However, the opposite is true for sea-ice area (and fraction). In HadISST1.1, the relationship of sea-ice area to sea-ice extent is very different before and after the 1970s. In HadISST2.1, which uses a more sophisticated method of deriving sea-ice area from sea-ice extent, their relationship is more consistent before and after the 1970s. That seems likely to be more realistic than the treatment in HadISST1.1, although given the very limited pre-1970s data available it is impossible to be sure which dataset more accurately represents the trend in Antarctic sea-ice area over 1871-2010.
Andrewsetal18 say that the fall in HadISST2.1 sea-ice area/fraction in the 1970s produces an unusual relationship between temperature and sea-ice area. However, the available data prior to the mid/late 1970s consists of sea-ice extent climatologies covering 1929-39 and 1947-62. It is possible that the actual decline in sea-ice extent and area started well before the 1970s, maybe as early as during the 1950s. Although global temperature if anything declined slightly from the 1950s to the late 1970s, high-latitude SH (50°S–60°S) SST rose strongly over that period, since when it has changed little. If the SH sea-ice fraction decline started in the 1950s, the sea-ice fraction trend over 1871-2010 would be little affected, but the relationship between temperature and sea-ice area over the 1960s and 1970s would be much less unusual.
In any event, whatever are the relative merits of the treatment of sea-ice in HadISST1 and HadISST2.1, the very different feedback strengths diagnosed from amipPiForcing simulations using the two datasets prove that the Andrewsetal18 main results are highly sensitive to the choice of SST and sea-ice dataset used, and therefore are too uncertain to draw any firm conclusions.
Figure 4. Monthly mean Southern Hemisphere sea-ice extent (solid) and area (dotted), for HadISST2.1 (black) and HadISST1.1 (red). The blue lines are not relevant.
Nicholas Lewis September 2018
[1] Lewis and Curry (2018) Table S2, for 31 CMIP5 models, based on the methods of estimating the two types of climate sensitivity described in Appendix A, with ECS estimated by regression over years 21-150 of an abrupt4xCO2 simulation. It is unknown to what extent, if any, a similar pattern effect occurs in the real climate system.
[2] Effective climate sensitivity is a proxy for equilibrium climate sensitivity – the rise on global surface temperature caused by a doubling of preindustrial CO2 concentration after the ocean equilibrates – derived from transient changes. Both in AOGCMs and the real climate system, EffCS is often estimated from changes in mean surface temperature and the difference between forcing and planetary radiative imbalance.
[3] Lewis, N. and J. Curry, 2018: The Impact of Recent Forcing and Ocean Heat Uptake Data on Estimates of Climate Sensitivity. J. Climate, 31, 6051–6071, doi:10.1175/JCLI-D-17-0667.1. Available here.
[4] Andrews T et al., 2018 Accounting for changing temperature patterns increases historical estimates of climate sensitivity. Geophys. Res. Lett. 10.1029/2018GL078887
[5] The paper refers to amipPiForcing simulations by eight AGCMs, but is only able to provide comparisons with their parent AOGCM’s response to CO2 forcing for six of them.
[6] Atmospheric Model Intercomparison Project (amip) simulations are a standard experimental protocol, in which an AGCM is driven by specified SST and sea-ice patterns. These patterns, and the atmospheric composition and other factors affecting radiative forcing, may be either fixed or evolving in time.
[7] Except for CAM4, which used constant year 2000 conditions. Land use is held constant in all cases.
[8] Feedback (λ) is measures how the planet’s radiative imbalance responds to a change in global mean surface temperature. The radiative imbalance is traditionally measured downward, so that a more highly negative λ (and so a greater absolute value of λ, | λ| or “feedback strength”) corresponds to a more strongly stabilizing climate system response.
[9] Lewis and Curry (2018) section 7c.
[10] Lewis and Curry (2018) section S4 / Table S2, and Armour (2017). Year 1 has been included in the regression here in order that the appropriate F2⤬CO2 values linking λamip and λhist values to effective climate sensitivities are very close. Generally, sensitivity estimates are almost the same whether regression is over years 1–50 or years 2–50 of abrupt4xCO2, or if derived from changes after 100 years in 1pctCO2 simulations (those in which CO2 concentration is increased at 1% per annum compound).
[11] Deriving λ by regression of the Earth’s annual global mean radiative imbalance on surface temperature.
[12] CAM4, CAM5.3, ECHAM6.3, GFDL-AM2.1, GFDL-AM3, GFDL-AM4.0, HadAM3 and HadGEM2. The GFDL simulations ran from 1870, with the AM2.1 and AM3 simulations ending in 2004; Andrewsetal18 discarded the year 1870 data.
[13] In AOGCMs, T and N are normally measured as anomalies relative to (i.e., changes from) their mean values in the same model’s preindustrial control simulation, sometimes adjusted for drift.
[14] To simplify comparisons, I have (as in Andrewsetal18) taken forcing for 4⤬ CO2 in CMIP5 models to be twice that for 2⤬ CO2. Computations in specialised models using slow but accurate radiation codes imply that in the real climate system it is about 2.09 times as high, but CMIP5 models use cruder, faster radiation codes and their 4⤬CO2 to 2⤬CO2 forcing ratio varies somewhat.
[15] ERF is the top-of-atmosphere (TOA) radiative forcing once stratospheric, tropospheric and other rapid climate system adjustments not related to surface temperature have taken place. It may be estimated using GCMs either from fixed-SST simulations or as the y-intercept of the regression line fit of N to T in a abrupt4xCO2 simulation. Such regression-based ERF estimates will however be biased downwards if the regression is affected by the decline in feedback strength that occurs in most AOGCMs a few decades into their abrupt4xCO2 simulations. It is standard to use ERF estimates, including for F2⤬CO2, when estimating EffCShist from observed warming.
[16] For the 31 CMIP5 GCMs considered in Lewis and Curry (2018), the mean F2⤬CO2 estimated from regression over years 1-50 of abrupt4xCO2 simulations is 3.80 Wm−2. That is the same as when estimated over years 2-10, a period starting after the rapid adjustments from instantaneous TOA radiative forcing to ERF have taken place and ending before feedback strength shows any noticeable decline. The mean F2⤬CO2 for the six AOGCMs featured in Table 1 estimated from regression over years 1-50 of their abrupt4xCO2 simulations is almost the same, at 3.74 Wm−2.
[17] The mean ERF F2⤬CO2 estimate of 3.80 Wm−2 referred to in the preceding endnote also agrees to a recent estimate of stratospherically-adjusted F2⤬CO2 using accurate radiation code (Etminan, M.et al, 2016. Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing. Geophys. Res. Lett. 43(24) doi:10.1002/2016GL071930). The IPCC AR5 report estimated ERF for CO2 to be the same as its stratospherically-adjusted radiative forcing.
[18] Titchner, H. A., and N. A. Rayner (2014), The Met Office Hadley Centre sea ice and sea surface temperature data set, version 2: 1. Sea ice concentrations, J. Geophys. Res. Atmos., 119, 2864–2889, doi:10.1002/2013JD020316.
[19] Andrewsetal18 term the original AMIP II, HadISST1 sea-ice based, simulations “amip-piForcing” and those based on the HadISST2 dataset “HadISST-piForcing”. However, both are atmosphere only simulations with preindustrial forcing, so we refer to both as amipPiForcing simulations.
[20] As it happens, that excess slightly exceeds both the mean and median ratio in CMIP5 AOGCMs of long-term CO2-forced effective sensitivity to ECShist.
[21] Estimating λamip and EffCSamip from the mean N and T anomalies (relative to the 1871-1900 mean) over the final 20 simulation years gives estimates substantially closer to those from regression (with intercept) using pentadal-mean data than using annual-mean data.
[22] Basing the models’ response to historical forcing on that in CO2-only forced simulations over a period providing a reasonable comparison to the evolution of forcing over the historical period.
[23] Andrewsetal18 say that in HadGEM2 the less negative feedback when changing dataset to HadISST2.1 is due to the positive shortwave (SW) clear-sky feedback nearly doubling.
[24] As in Andrewsetal18, anomalies for abrupt4⤬CO2 simulations are relative to values in the same coupled model’s preindustrial control, while those in the atmosphere-only amipPiForcing simulations are relative to the 1871-1900 mean in the same simulation.
[25] IPCC AR5 WG1 Table 9.5.
[26] Gregory, J. M., and T. Andrews, 2016: Variation in climate sensitivity and feedback parameters during the historical period. Geophys. Res. Lett., 43: 3911–3920.
[27] Testing is based on detrended T and N values for all 18,391 140-year long segments from 43 archived CMIP5 model preindustrial control run simulations. For each model, ensemble mean N from its amipPiForcing simulations is compared with that derived from T in the same simulations and detrended values NIV and TIV from each piControl simulation segment in turn. For each thus generated realization of internal variability, ΔN is computed as λhist (ΔT − ΔTIV) + ΔNIV, changes Δ being mean anomalies for the final 15 years of the amipPiForcing experiment, as in Lewis and Curry (2018), with the anomalization period being the first 30 years. Using means over the final 20 rather than 15 years gives the same result. For the ECHAM6.3/MPI-ESM1.1 model, its estimated λamip value of –1.90 Wm−2 °C−1 can be compared with the actual λhist values in its ensemble of 100 historical simulations. Those λhist values, estimated from changes between the first and last 20 years of the historical simulations, ranged between 1.04 and 1.52 Wm−2 °C−1, with a median of 1.30 Wm−2 °C−1.
[28] Armour (2017) found that averaging responses over years 85-115 of 1pctCO2 simulation provided a good proxy for EffCShist. Lewis and Curry (2018) showed that for 31 CMIP5 models their ensemble-mean ECShist estimated from years 85–115 of 1pctCO2 simulations (during which the average age of forcing increments is fifty years) and from regression over years 2–50 of abrupt4xCO2 simulations differ by under 1%.
[29] Lewis and Curry (2018) showed that in the GISS-E2-R model ECShist estimated from historical simulations very marginally exceeded ECShist estimated from years 85–115 of 1pctCO2 simulations. For the other model for which I have been able to obtain historical simulation effective radiative forcing data (MPI-ESM1.1, which incorporates almost the same ECHAM6.3 atmospheric model as that used in Andrewsetal18), ECShist estimated from historical simulations (2.72°C per Dessler et al. 2018 DOI: 10.5194/acp-18-5147-2018; I estimate marginally under 3°C) is insignificantly different from ECShist estimated by regressing over years 2–50 of the almost identical MPI-ESM1.2 model’s abrupt2xCO2 simulation (2.62°C).
[30] Armour, K. C., 2017: Energy budget constraints on climate sensitivity in light of inconstant climate. feedbacks. Nature Climate Change, 7, 331-335.
[31] Geoffroy, O., Saint-Martin, D., Bellon, G., Voldoire, A., Olivié, D. J. L., & Tytéca, S. (2013). Transient climate response in a two-layer energy-balance model. Part II: Representation of the efficacy of deep-ocean heat uptake and validation for CMIP5 AOGCMs. Journal of Climate, 26(6), 1859-1876.
[32] Proistosescu, C; P Huybers ,2017. Slow climate mode reconciles historical and model-based estimates of climate sensitivity. Sci Adv 3: e1602821.
[33] For the 31 CMIP5 models investigated in Lewis and Curry (2018). The medians for the two measures are close to each other.
[34] For instance, in the GFDL models used in the paper, regression over years 21–150 of their abrupt4xCO2 simulations materially underestimates their true ECS; in the UKMO HadGEM2-ES model it appears to materially overestimate it, and in the MPI model it appears to estimate it fairly accurately. Even running a model forced by CO2 change to equilibrium does not necessarily give an accurate estimate of its true ECS, since model variables drift (due, e.g., to energy leakage) and such drift may be time and/or temperature dependent.
[35] The range does not include uncertainty in the estimates of EffCShist and ECS. In the real climate system the ECS-to- EffCShist ratio could in any event be outside its range in CMIP5 models.
[36] Mauritsen, T., and R. Pincus, 2017: Committed warming inferred from observations. Nature Climate Change, 7(9), nclimate3357.
[37] Based on the Lewis and Curry (2018) EffCShist estimates.
[38] While a corresponding simulation with doubled CO2 does not appear to have been carried out using the MPI-ESM1.1 version, a 2,600 year long abrupt4xCO2 simulation has been. Results using the first 1000 years’ data are almost identical to those from the 1000-year abrupt4xCO2 simulation using MPI-ESM1.2, while the long term sensitivity estimate increases by only ~2% between years 1000 and 2600.
[39] Estimating λ either from changes between means for the first and last ten years of the historical simulations or from annual regression over them, at −1.34 Wm−2K−1 in both cases. Data from the first two simulation years was discarded since the forcing estimates for those years appear to be anomalously low.
[40] ECShist is estimated from the ensemble-mean of historical simulation data at 2.16 K (Lewis and Curry 2018 sections 7c and S3) and its Deming-regression derived long term ECS as 2.27 K. No adjustment has been made for 4⤬ CO2 forcing being slightly more than double 2⤬ CO2 forcing, as that does not appear to be the case in GISS-E2-R.
[41] Tim Andrews has helpfully provided me with the HadGEM2 HadISST2.1-based amipPiForcing global T and N data. I have not as yet been able to obtain the corresponding data for HadAM3.
[42] The HadISST1 1871–2010 trend weakens by 1% when 1970s data is excluded.
[43] Titchner, H. A., and N. A. Rayner (2014), The Met Office Hadley Centre sea ice and sea surface temperature data set, version 2: 1. Sea ice concentrations, J. Geophys. Res. Atmos., 119, 2864–2889
Leave A Comment