A pdf copy of this article is available here

Christopher Snowdon makes some reasonable points in his 16 January 2021 article in Quillette “Rise of the Coronavirus Cranks”. However, he conflates cranks and rational sceptics, resulting in much of his critique being wide of the mark or plain wrong, and rational sceptics being unfairly tarred with the same brush as cranks. A response to Snowdon’s general argument has since been published elsewhere, however it does not challenge the key quantitative criticism that Snowdon makes.

Snowdon asserts that claims by Mike Yeadon are “demonstrably nonsensical”. Specifically, he attacks Yeadon’s claim in an article written in mid-September 2020, that the vast majority of Covid cases identified by Pillar 2 (testing in the community, England) since May 2020 had been false positives. Snowdon accepts the mathematics but challenges Yeadon’s assumptions regarding the true positive rate and the PCR test false positive rate, of 0.1% (the rate found by the Office of National Statistics) and 0.8% (the low end of a 0.8–4.0% false positive rate range stated in a report by government scientists).

Snowdon wrote that Yeadon “did not draw the obvious conclusion that if the false positive rate of the PCR test was 0.8 percent, the ONS should find positives at least 0.8 percent of the time.” Snowdon may think that is an obvious conclusion, but unfortunately that just reveals his scientific and statistical ignorance. As I will show, what Snowdon thinks is an ‘obvious conclusion’ is actually false.

Both the ONS and Imperial College’s REACT study assess Covid prevalence by measuring the proportion of randomly selected individuals in England with positive results for PCR tests processed by high quality, well established laboratories. Moreover, REACT does not count certain marginal tests results as positive. That results in a very low false positive rate, of no more than 0.033% (the lowest test positivity rate in any REACT survey). On the same basis, the false positive rate for the ONS study cannot exceed 0.06%. When Yeadon prepared his article, the latest ONS and REACT surveys showed test positivity rates of 0.076% and 0.089% respectively, with the ONS modelled estimate for the final week of the sampling period being 0.11%. So Yeadon’s assumption of a 0.1% true positivity rate in the community seems very reasonable.

However, unlike the ONS and REACT surveys, Pillar 2 uses high volume ‘Lighthouse’ laboratories to process its tests. These were newly set up and under pressure to increase volumes. They appear to generally be substantially lower quality than the well established laboratories used by the ONS and REACT, with implications for false positive rates. Serious failings were identified in one Lighthouse lab., giving rise to risk of cross-contamination of samples. At another Lighthouse lab., working practices were described as “chaotic and dangerous”. The same lab. was also revealed to have suffered Covid outbreaks in three of its four testing teams, which could have further increased false positives. Even in a Lighthouse lab. set up by partners possessing exceptional expertise (University of Cambridge, Astrazeneca and GSK) and with no reported issues, mass testing of students, and retesting them where initial tests were positive, revealed a false positive rate of 0.3%.

As Snowdon says, people are not tested at random in Pillar 2, with many displaying symptoms that could be of Covid, and one would therefore expect a higher proportion of them to have Covid than under the random testing in the ONS and REACT studies. However, one would expect Pillar 2 positivity rates to be strongly correlated with those in the community. Indeed, until the second lockdown, the correlation between Pillar 2 test positivity rates and those in REACT testing rounds is virtually perfect: 0.9999. As the chart shows, changes in Pillar 2 positivity rates were 8.5 times greater than changes in REACT positivity rates.

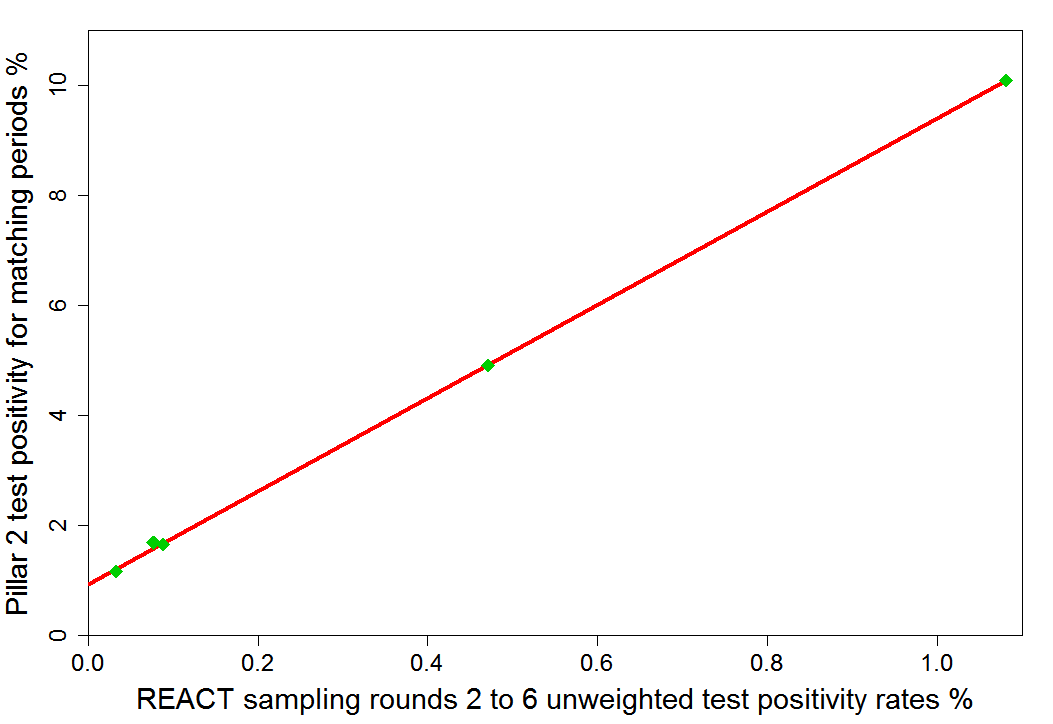
One can use this very tight statistical relationship and the very low REACT false positivity rate to derive good estimates for the false positive rates in Pillar 2 testing. Those estimates increase only marginally with the assumed false positive rate for REACT testing. The REACT false positive rate, while unknown, must be positive and not more than 0.033%. I make the neutral assumption that it is half that level. The implied false positive rate for Pillar 2 testing then fluctuates in a narrow range just above 1.0%, from late June until Lockdown 2. So, while there are obviously uncertainties in this estimate, Yeadon’s assumption of a 0.8% Pillar 2 false positive rate appears if anything to be on the low side.

Using the derived false positive rate estimates for Pillar 2 testing (interpolated between REACT sampling periods), one can test Yeadon’s claim that the vast majority of cases identified by Pillar 2 since May 2020 were false positives. I exclude the first three weeks of Pillar 2 data, which have little overlap with REACT data, and weeks for which no Pillar 2 data was available when Yeadon made his claim. I thereby calculate that over the period 18th June to 2nd September 2020 approximately one in seven Pillar 2 positive test results had been true. So Yeadon’s claim appears reasonable. A low proportion in the summer of positive PCR test results that were true has also been reported elsewhere. Moreover, an unknown but quite likely substantial proportion of ‘true positives’ represent the detection merely of harmless fragments of viral RNA, or of complete viruses in too low a concentration to be infectious. It is true that the proportion of false positive test results becomes much smaller when infection is more prevalent, but that is not relevant to Yeadon’s claim.

Snowdon claimed that “Fewer than a thousand tests a day were coming back positive in July, but by the time Yeadon’s article appeared, they were exceeding 5,000. The number of tests performed each day had nearly doubled in this period, but that could not explain a fivefold increase in reported case numbers.” But 5,000 was the daily rate for all tests, whereas Yeadon was specifically referring to Pillar 2 testing. When his article appeared, the latest published Pillar 2 was for the week to 2 September 2020.  More complete data published subsequently show that the Pillar 2 test positivity rate rose from 1.2% in the last week in July to 1.5% in the week to 2 September, a ratio of only 1.28 times.

None of this casts doubt on the subsequent strong rise in the prevalence of Covid. Nor of course does it imply that all assertions by rational sceptics are valid. But the fact that Snowdon went totally wrong on his central scientific criticism indicates  that his thinking on other points, including the merits of the current lockdown, may also be faulty.

 

Nicholas Lewis                                                                      31 January 2021