Originally a guest post on Mar 2, 2016 – 8:56 AM at Climate Audit
Introduction
In April 2014 I published a guest article about statistical methods applicable to radiocarbon dating, which criticised existing Bayesian approaches to the problem. A standard – subjective Bayesian – method of inference about the true calendar age of a single artefact from a radiocarbon date determination (measurement) involved using a uniform-in-calendar-age prior. I argued that this did not, as claimed, equate to not including anything but the radiocarbon dating information, and was not a scientifically sound method for inference about isolated examples of artefacts.[1]
My article attracted many comments, not all agreeing with my arguments. This article follows up and expands on points in my original article, and discusses objections raised.
First, a brief recap. Radiocarbon dating involves determining the radiocarbon age of (a sample from) an artefact and then converting that determination to an estimate of the true calendar age t, using a highly nonlinear calibration curve. It is this nonlinearity that causes the difficulties I focussed on. Both the radiocarbon determination and the calibration curve are uncertain, but errors in them are random and in practice can be combined. A calibration program is used to derive estimated calendar age probability density functions (PDFs) and uncertainty ranges from a radiocarbon determination.
The standard calibration program OxCal that I concentrated on uses a subjective Bayesian method with a prior that is uniform over the entire calibration period, where a single artefact is involved. Calendar age uncertainty ranges for an artefact whose radiocarbon age is determined (subject to measurement error) can be derived from the resulting posterior PDFs. They can be constructed either from one-sided credible intervals (finding the values at which the cumulative distribution function (CDF) – the integral of the PDF – reaches the two uncertainty bound probabilities), or from highest probability density (HPD) regions containing the total probability in the uncertainty range.
In the subjective Bayesian paradigm, probability represents a purely personal degree of belief. That belief should reflect existing knowledge, updated by new observational data. However, even if that body of knowledge is common to two people, their probability evaluations are not required to agree,[2] and may for neither of them properly reflect the knowledge on which they are based. I do not regard this as a satisfactory paradigm for scientific inference.
I advocated taking instead an objective Bayesian approach, based on using a computed “noninformative prior” rather than a uniform prior. I used as my criterion for judging the two methods how well they performed upon repeated use, hypothetical or real, in relation to single artefacts. In other words, when estimating the value of a fixed but unknown parameter and giving uncertainty ranges for its value, how accurately would the actual proportions of cases in which the true value lies within each given range correspond to the indicated proportion of cases? That is to say, how good is the “probability matching” (frequentist coverage) of the method. I also examined use of the non-Bayesian signed root log-likelihood ratio (SRLR) method, judging it by the same criterion.
Bayesian parameter inference
A quick recap on Bayesian parameter inference in the continuously-valued case, which is my exclusive concern here. In the context we have here, with a datum – the measured C14 age (radiocarbon determination) dC14 – and a parameter t, Bayes’ theorem states:
p(t|dC14) = p(dC14|t) p(t) / p(dC14) (1)
where p(x|y) denotes the conditional probability density for variable x given the value of variable y. Since p(dC14) is not a function of t, it can be (and usually is) replaced by a normalisation factor set so that the posterior PDF p(t|dC14) integrates to unit probability. The probability density of the datum taken at the measured value, expressed as a function of the parameter (the true calendar age t), p(dC14|t), is called the likelihood function. The construction and interpretation of the prior distribution or prior, p(t), is the critical practical difference between subjective and objective Bayesian approaches. In a subjective approach, the prior represents as a probability distribution the investigator’s existing degree of belief regarding varying putative values for the parameter being estimated. There is no formal requirement for the choice of prior to be evidence-based, although in scientific inference one might hope that it often would be. In an objective approach, the prior is instead normally selected to be noninformative, in the sense of letting inference for the parameter(s) of interest be determined, to the maximum extent possible, solely by the data.
A noninformative prior primarily reflects (at least in straightforward cases) how informative, at differing values of the parameter of interest, the data are expected to be about that parameter. In the univariate parameter continuous case, Jeffreys’ prior is known to be the best noninformative prior, in the sense that, asymptotically, Bayesian posterior distributions generated using it provide closer probability matching than those resulting from any other prior.[3] Jeffreys’ prior is the square root of the (expected) Fisher information. Fisher information – the expected value of the negative second derivative of the log-likelihood function with respect to the parameters, in regular cases – is a measure of the amount of information that the data, on average, carries about the parameter values. In simple univariate cases involving a fixed, symmetrical measurement error distribution, Jeffreys’ prior will generally be proportional to the derivative of the data variable being measured with respect to the parameter.
To simplify matters, I worked with a stylised calibration curve, which conveyed key features of the nonlinear structure of the real calibration curve – alternating regions where the radiocarbon date varied rapidly and very slowly with calendar age – whilst retaining strict monotonicity and having a simple analytical derivative. Figure 1, a version of Figure 2 in the original article, shows the stylised calibration curve (black) along with the error distribution density for an example radiocarbon date determination (orange). The grey wings of the black curve represent a fixed calibration curve error, which I absorb into the C14 determination error, assumed here to have a Gaussian distribution with fixed, known, standard deviation. The solid pink line shows the Bayesian posterior probability density function (PDF) using a uniform in calendar age prior. The dotted green line shows the noninformative Jeffreys’ prior used in the objective Bayesian method, which reflects the derivative of the calibration curve. The posterior PDF using Jeffreys’ prior is shown as the solid green line. The dashed pink and green lines, added in this version, show the corresponding posterior CDF in each case.
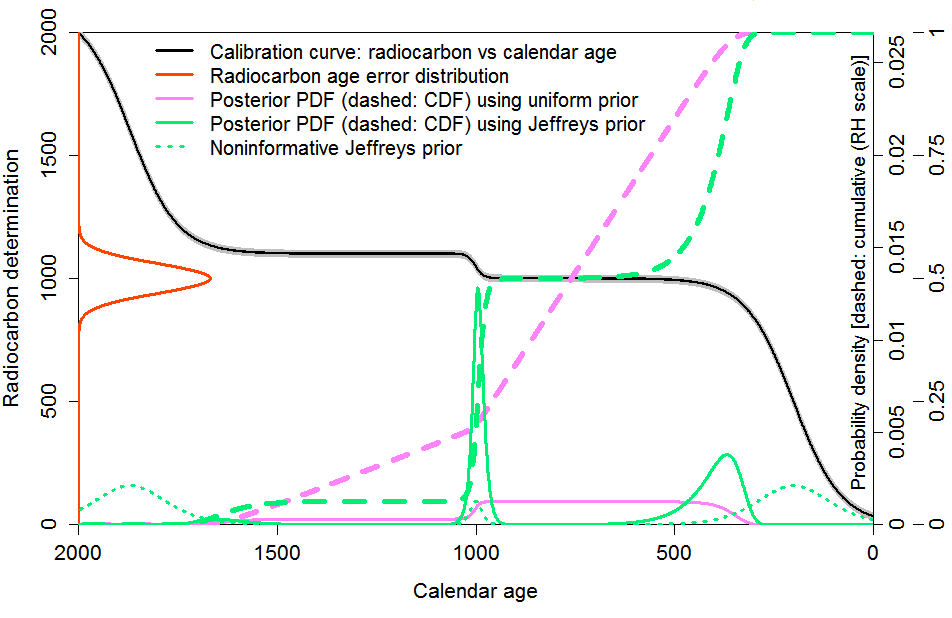
an example observation; combined measurement/calibration error standard deviation 60 RC years.
The shape of the objective Bayesian posterior PDF
The key conclusions of my original article were:
“The results of the testing are pretty clear. In whatever range the true calendar age of the sample lies, both the objective Bayesian method using a noninformative Jeffreys’ prior and the non-Bayesian SRLR method provide excellent probability matching – almost perfect frequentist coverage. Both variants of the subjective Bayesian method using a uniform prior are unreliable. The HPD regions that OxCal provides give less poor coverage than two-sided credible intervals derived from percentage points of the uniform prior posterior CDF, but at the expense of not giving any information as to how the missing probability is divided between the regions above and below the HPD region. For both variants of the uniform prior subjective Bayesian method, probability matching is nothing like exact except in the unrealistic case where the sample is drawn equally from the entire calibration range”
For many scientific and other users of statistical data, I think that would clinch the case in favour of using the objective Bayesian or the SRLR methods, rather than the subjective Bayesian method with a uniform prior. Primary results are generally given by way of an uncertainty range with specified probability percentages, not in the form of a PDF. Many subjective Bayesians appear unconcerned whether Bayesian credible intervals provided as uncertainty ranges even approximately constitute confidence intervals. Since under their interpretation probability merely represents a degree of belief and is particular to each individual, perhaps that is unsurprising. But, in science, users normally expect such ranges to be at least approximately valid as confidence intervals, so that, upon repeated applications of the method – not necessarily to the same parameter – in the long run the true value of the parameter being estimated would lie within the stated intervals in the claimed percentages of cases.
However, there was quite a lot of pushback against the rather peculiar shape of the objective Bayesian posterior PDF resulting from use of Jeffreys’ prior. It put near zero probability on regions where the data, although being compatible with the parameter value, was insensitive to it. That is, regions where the data likelihood was significant but the radiocarbon determination varied little with calendar age, due to the flatness of the calibration curve. The pink, subjective Bayesian posterior PDF was generally thought by such critics to be more realistically-shaped. Underlying that view, critics typically thought that there was relevant prior information about the age distribution of artefacts that should be incorporated, by reflecting through use of a uniform prior a belief that an artefact was equally likely to come from any (equal-length) calendar age range. Whether or not that is so, the uniform prior had instead been chosen on that basis that it did not introduce anything but the RC dating information, and I argued against it on that basis.
I think the view that one should reject an objective Bayesian approach just on the basis that the posterior PDF is gives rise to is odd-looking is mistaken. In most cases, what is of concern when estimating a fixed but uncertain parameter, here calendar age, is how well one can reliably constrain its value within one or more uncertainty ranges. In this connection, it should be noted that although the Jeffreys’ prior will assign low PDF values in a range where likelihood is substantial but the data variable is insensitive to the parameter value, the uncertainty ranges that the resulting PDF gives rise to will normally include that range.
Probability matching
I think it is best to work with one-sided ranges, which unlike two-sided ranges are uniquely defined, whereas an 80% (say) range could be 5–85% or 10–90%. A one-sided x% range is the range from the lowest possible value of the parameter (here, zero) to the value, y, at which the range contains x% of the posterior probability. An x1–x2% range or interval for the parameter is then y1 − y2, where y1 and y2 are the (tops of the) one-sided x1% and x2% ranges. An x% one-sided credible interval derived from a posterior CDF relates to Bayesian posterior probability. By contrast, a (frequentist) x% one-sided confidence interval bounded above by y is calculated so that, upon indefinitely repeated random sampling from the data uncertainty distribution(s) involved, the true parameter value will lie below the resulting y in x% of cases (i.e., with a probability of x%).
By definition, an accurate confidence interval bound exhibits exact probability matching. If one-sided Bayesian credible intervals derived using a particular prior pass the matching test for all values of x then they and the prior used are said to be probability matching. From a scientific viewpoint, probability matching is highly desirable. It implies – if the statistical analyses have been performed (and error distributions assessed) correctly – that, for example, only in one study out of twenty will the true parameter value lie above the reported 95% uncertainty bound. In general, Bayesian posteriors can only, at best, be approximately probability matching. But the simple situation presented here falls within the “location parameter” exception to the no-exact-probability-matching rule, and use of Jeffreys’ prior should in principle lead to Bayesian one-sided credible intervals exhibiting exact probability matching.
The two posterior PDFs in Figure 1 imply very different calendar age uncertainty ranges. However, as I showed in the original article, if a large number of true calendar ages are sampled in accordance with the assumed uniform distribution over the entire calibration curve (save, to minimise end-effects from likelihood lying outside the calibration range, 100 years at each end), and a radiocarbon date determined for each of them in accordance with the calibration curve and error distribution, then both methods provide excellent probability matching. This is to be expected, but for different reasons in the subjective and objective Bayesian cases.
Figure 2, a reproduction of Figure 3 in the original article, shows the near perfect probability matching in this case for both methods. At all one-sided credible/confidence interval sizes (upper level in percent), the true calendar age lay below the calculated limit in almost that percentage of cases. As well as results for one-sided intervals using the subjective Bayesian method with a uniform prior and the objective Bayesian method with Jeffreys’ prior, Figure 2 shows comparative results on two other bases. The blue line is for two-sided HPD regions, using the subjective Bayesian method with a uniform prior. An x% HPD region is the shortest interval containing x% of the posterior probability and in general does not contain an equal amount of probability above and below the 50% point (median). The dashed green line uses the non-Bayesian signed root log-likelihood ratio (SRLR) method, which produces confidence intervals that are in general only approximate but are exact when a normal distribution or a transformation thereof is involved, as here.
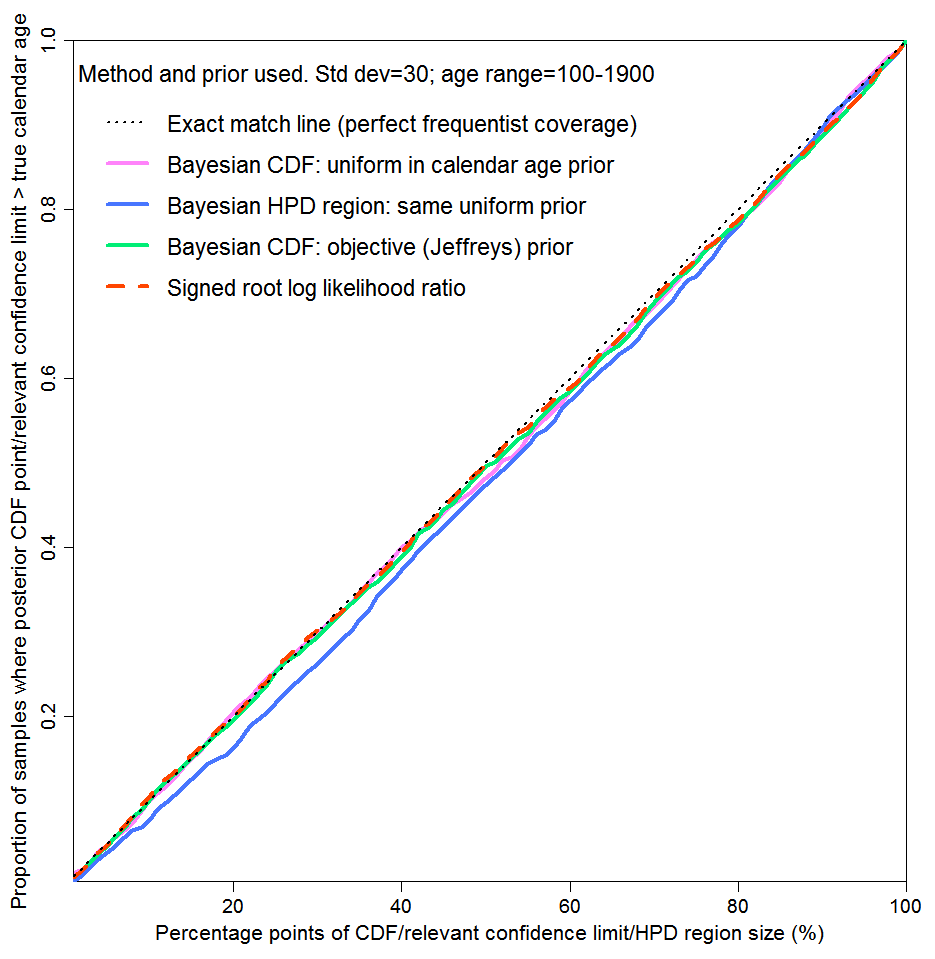
Figure 2 supports use of a subjective Bayesian method in a scenario where there is an exactly known prior probability distribution for the unknown variable of interest (here, calendar age), many draws are made at random from it and only probability matching averaged across all draws is of concern. The excellent probability matching for the subjective Bayesian method shows that stated uncertainty bounds using it are valid when aggregated over samples of parameter values drawn randomly, pro rata to their known probability of occurring. In such a case, Bayes’ theorem follows from the theory of conditional probability, which is part of probability theory as rigorously developed by Kolmogorov.[4]
However, the problem of scientific parameter inference is normally different. The value of a parameter is not drawn from a known probability distribution, and does not vary randomly from one occasion to another. It has a fixed, albeit unknown, value, which is the target of inference. The situation is unlike the scenario where the distribution from which parameter values are drawn is fixed but the parameter value varies between draws, and, often, no one drawn parameter value is of particular significance (a “gambling scenario”). Uncertainty bounds that are sound only when parameter values are drawn from a known probability distribution, and apply only upon averaging across such draws, are not normally appropriate for scientific parameter inference. What is wanted are uncertainty bounds that are valid on average when the method is applied in cases where there is only one, fixed, parameter value, and it has not been drawn at random from a known probability distribution.
In Figure 2, values for the unknown variable are drawn many times at random from a specified distribution and in each instance a single subject-to-error observation is made. The testing method corresponds to a gambling scenario: it is only the average probability matching over all the parameter values drawn that matters. Contrariwise, Figure 3 corresponds to the parameter inference case, where probability matching at each possible parameter value separately matters. I selected ten possible parameter values (calendar ages), to illustrate how reliable inference would typically be when only a single, fixed, parameter value is concerned. I actually drew the parameter values at random, uniformly, from the same age range as in Figure 2, but I could equally well have chosen them in some other way. For each of these ten values, I drew 5,000 radiocarbon date determinations randomly from the measurement error distribution, rather than a single draw as used for Figure 2, and computed one-sided 1% to 100% uncertainty intervals. Each of the lines corresponds to one of the ten selected parameter values.
As can be seen, the objective Bayesian and the SRLR methods again provide almost perfect probability matching in the case of each of the ten parameter values separately (the differences from exact matching are largely due to end effects). But probability matching for the subjective Bayesian method using a uniform prior was poor – awful over much of the probability range in most of the ten cases. Whilst HPD region coverage appears slightly less bad than for one-sided intervals, only the total probability included in the HPD region is being tested in this case: the probabilities of the parameter value lying above the HPD region and lying below it may be very different from each other. Therefore, HPD regions are useless if one wants the risks of over- and under-estimating the parameter value to be similar, or if one is primarily concerned about one or other of those risks.
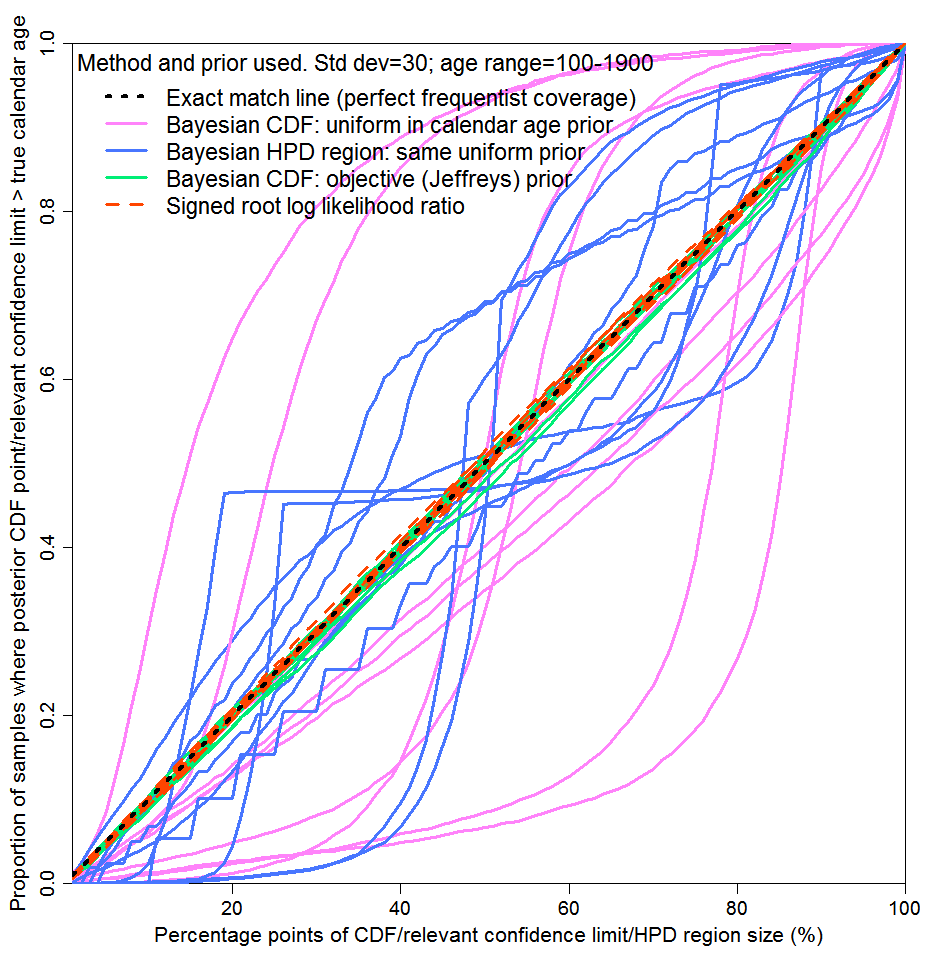
from a uniform distribution: 5000 C14 measurements for each
I submit that Figure 3 strongly supports my thesis that a uniform prior over the calibration range should not be used here for scientific inference about the true calendar age of a single artefact, notwithstanding that it gives rise to a much more intuitively-appealing posterior PDF than use of Jeffreys’ prior. It may appear much more reasonable to assume such a uniform prior distribution than the highly non-uniform Jeffreys’ prior. However, the wide uniform distribution does not convey any genuine information. Rather, it just causes the posterior PDF, whilst looking more plausible, to generate misleading inference about the parameter.
What if an investigator is only concerned with the accuracy of uncertainty bounds averaged across all draws, and the artefacts are known to be exactly uniformly distributed? In that case, is there any advantage in using the subjective Bayesian method rather than the objective one, apart from the posterior PDFs looking more acceptable? Although both methods deliver essentially perfect probability matching, one might generate uncertainty intervals that are, on average, smaller than those from the other method, in which case it would arguably be superior. Re-running the Figure 2 case did indeed reveal a difference. The average 5–95% uncertainty interval was 736 years using the objective Bayesian method. It was rather longer, at 778 years, using the subjective Bayesian method.
So in this case the objective Bayesian method not only provides accurate probability matching for each possible parameter value, but on average it generates narrower uncertainty ranges even in the one case where the subjective method also provides probability matching. Even the less useful HPD 90% regions, which say nothing about the relative chances of the parameter value lying below or above the region, were on average only slightly narrower, at 724 years, than the objective Bayesian 5–95% regions. The failure of the subjective Bayesian method to provide narrower 5–95% uncertainty ranges reflects the fact that knowing the parameter is drawn randomly from a wide uniform distribution provides negligible useful information about its value.
Is standard usage of Bayes’ theorem appropriate for parameter inference?
My tentative interpretation of the difference between inference using a uniform prior in Figures 2 and 3 is this. In the Figure 2 case, the calendar age is a random variable, in the Kolmogorov sense (a KRG). Each trial involves drawing an artefact, and for it an associated RC determination, at random. There is a joint probability function involved and a known unconditional probability distribution for calendar age. The conditional probability density of calendar age for an artefact given its RC determination is then well defined, and given by Bayes’ theorem. But in the Figure 3 case, taking any one of the ten selected calendar ages on their own, there is no joint probability distribution involved. The parameter (calendar age) is not a KRG;[5] its value is fixed, albeit unknown. A conditional probability density for the calendar age of the artefact is therefore not validly given, by Bayes’ theorem, as the product of its unconditional density and the conditional density of the RC determination, since the former does not exist.[6]
Under the subjective Bayesian interpretation, the standard use of Bayes’ theorem is always applicable for inference about a continuously-valued fixed but unknown parameter In my view, Bayes’ theorem may validly be applied in the standard way in a gambling scenario but not, in general, in the case of scientific inference about a continuously-valued fixed parameter – although it will provide valid inference in some cases and lead only to minor error in many others. The fact that the standard subjective uses of Bayes’ theorem should never lead to internal inconsistencies in personal belief systems does not mean that they are objectively satisfactory.
Preliminary conclusions
If there are many realisations of the variable of interest, drawn randomly from a known probability distribution, and inferences made after obtaining observational evidence for each value drawn only need to be valid when aggregated across all the draws, then a subjective Bayesian approach produces sound inference. By sound inference, I mean here that uncertainty statements in the form of credible intervals derived from posterior PDFs exhibit accurate probability matching when applied to observational data relating to many randomly drawn parameter values. Moreover, the posterior PDFs produced have a natural probabilistic interpretation.
However, if the variable of interest is a fixed but unknown, unchanging parameter, subjective Bayesian inferences are in principle objectively unreliable, in the sense that they will not necessarily produce good probability matching for multiple draws of observational data with the parameter value fixed. Not only is aggregation across randomly drawn parameter values impossible here, but only the value of the actual, fixed, parameter is of interest. In such cases I suggest that most researchers using a method want it to produce uncertainty statements that are, averaged over multiple applications of the method in the same or comparable types of problem, accurate. That is to say, their uncertainty bounds constitute, at least approximately, confidence intervals.[7] In consequence, the posterior PDFs produced by such methods will be close to confidence densities.[8] It follows that they may not necessarily have a natural probabilistic interpretation, so the fact that their shapes may not appear to be realistic as estimated probability densities is of questionable relevance, at least for estimating parameter values.
Subjective Bayesians often question the merits of confidence intervals. They point out that “relevant subsets” may exist, which can lead to undesirable confidence intervals. But I think the existence of such pathologies is in practice rare, or easily enough overcome, where a continuous fixed parameter is being estimated. Certainly, the suggestion in a paper recommended to me by a fundamentalist subjective Bayesian statistician active in climate science, that the widely used Student’s t-distribution involves relevant subsets, seems totally wrong.
To summarise, I still think objective Bayesian inference is normally superior to subjective Bayesian inference for scientific parameter estimation, but the posterior PDFs it generates may not necessarily have the usual probabilistic interpretation. I plan, in a subsequent article, to discuss how to incorporate useful, evidence based, probabilistic prior information about the value of a fixed but unknown parameter using an objective Bayesian approach.
Nicholas Lewis
Notes and References
[1] I did not comment on the formulation of priors for inference about groups of artefacts (which was a major element of the standard methodology involved).
[2] De Finetti, B. ,2008. Philosophical lectures on probability, Springer, 212 pp. p.23
[3] Welch, B L, 1965. On comparisons between confidence point procedures in the case of a single parameter. J. Roy. Soc. Ser. B, 27, 1, 1-8; Hartigan, 1965.The Asymptotically Unbiased Prior Distribution, Ann. Math. Statist., 36, 4, 1137-1152
[4] Kolmogorov, A N, 1933, Foundations of the Theory of Probability. Second English edition, Chelsea Publishing Company, 1956, 84 pp.
[5] Barnard, GA, 1994: Pivotal inference illustrated on the Darwin Maize Data. In Aspects of Uncertainty, Freeman, PR and AFM Smith (eds), Wiley, 392pp.
[6] Fraser, D A S, 2011. Is Bayes Posterior just Quick and Dirty Confidence? Statistical Science, 26, 3, 299–316.
[7] There is a good discussion of confidence and credible intervals in the context of Bayesian analysis using noninformative priors in Section 6.6 of J O Berger (1980): Statistical decision theory and Bayesian analysis, 671pp.
[8] Confidence densities are discussed in Schweder T and N L Hjort, 2002: Confidence and likelihood. Scandinavian Jnl of Statistics, 29, 309-332.
Leave A Comment