Originally a guest post on Feb 5, 2015 – 10:42 AM at Climate Audit
Introduction
A new paper in Nature by Jochem Marotzke and Piers Forster: ‘Forcing, feedback and internal variability in global temperature trends’[i] investigates the causes of the mismatch between climate models that simulate a strong increase in global temperature since 1998 and observations that show little increase, and the influence of various factors on model-simulated warming over longer historical periods. I was slightly taken aback by the paper, as I would have expected either one of the authors or a peer reviewer to have spotted the major flaws in its methodology. I have a high regard for Piers Forster, who is a very honest and open climate scientist, so I am sorry to see him associated with a paper that I think is very poor, even as co-author (a position that perhaps arose through him supplying model forcing data to Marotzke) and therefore not bearing primary responsibility for the paper’s shortcomings.
In putting together this note, I have had the benefit of input from two statistical experts: Professor Gordon Hughes (Edinburgh University) and Professor Roman Mureika (University of New Brunswick, now retired). Both of them regard the statistical methods in Marotzke’s paper as fatally flawed.
The Marotzke and Forster paper analyses trends in simulated global mean surface temperature (GMST) over all 15- and 62-year periods between 1900 and 2012, and relates them to contemporaneous trends in model effective radiative forcing (ERF) and to measures of model feedback strength (alpha) and model ocean heat uptake efficiency (kappa).
The paper is very largely concerned with the behaviour of climate models, specifically atmosphere-ocean general circulation models used in the CMIP5 simulations. In discussing relevance to the actual climate system, it ‘assumes that the simulated multimodel ensemble spread accurately characterizes internal variability’.
The authors’ principal conclusions are:
The differences between simulated and observed trends are dominated by random internal variability over the shorter timescale and by variations in the radiative forcings used to drive models over the longer timescale. For either trend length, spread in simulated climate feedback leaves no traceable imprint on GMST trends or, consequently, on the difference between simulations and observations. The claim that climate models systematically overestimate the response to radiative forcing from increasing greenhouse gas concentrations therefore seems to be unfounded.
Marotzke claims to have shown that in model simulations the structural (alpha and kappa) elements – which encapsulate model GMST responses to increases in CO2 forcing – contributed nothing even to recently-ending, longer-term GMST trends. It is difficult to see how that can be so if the models work properly. It is certainly possible (in fact likely) that over the period 1900–2012 the combined contribution of alpha and kappa to model GMST trends was largely obscured by countervailing variations in model ERF trends: high sensitivity models tend to have more negative aerosol forcing than lower sensitivity models, enabling both to match 20th century GMST trends. But aerosol levels have changed little over the last 35 years and higher sensitivity models have been warming much faster than observed GMST over that period.
In order to show why the paper’s conclusions are not justified, I need to explain what Marotzke has done.
What Marotzke did
Marotzke starts with a ‘physical foundation’ of energy balance: ΔT = ΔF / (α + κ), where ΔF is the change in ERF; α is the climate feedback parameter (the reciprocal of equilibrium/effective climate sensitivity [ECS] normalised by F2xCO2, the ERF from a doubling of CO2 concentration: α = F2xCO2/ECS ); κ is the ratio of change in the rate of heat uptake by the climate system – or in its counterpart, top-of-atmosphere (TOA) radiative imbalance – to change in GMST, termed ocean heat uptake efficiency; and ΔT is the change in GMST.[ii]
Marotzke then adds a random term, ε, to represent internal variability in GMST, resulting in the equation
. ΔT = ΔF / (α + κ) + ε (1)
which is taken to apply to linear trends, rather than changes, in GMST and ERF.
He then takes temperature data and individual ERF time series relating to their historical simulations[iii] from an ensemble of 18 CMIP5 models.[iv] The ERF time series were not included in the model simulation output but had previously been diagnosed (estimated) therefrom by Forster et al, along with values for α and κ.
Marotzke expresses each quantity in (1) as where the overbar represents the ensemble mean and the prime the across-ensemble variation. By considering a linear expansion of equation (1), using those expressions, he arrives at the approximation
Marotzke states that this equation suggests a regression model
where the value of j identifies the particular model run involved. Some models have multiple simulation runs, but each model’s values for ΔF, α and κ are common to all its runs.
I’m rather dubious about the validity of the approximations used in (2) given that α is typically somewhat larger than κ and there is nearly a threefold variation in α across the models, meaning that many of the α’ terms are substantial in relation to the model ensemble mean. But I will leave that aside for the present purposes.
Marotzke performs multiple linear regressions according to the statistical model (3) for each start year (1900–1998 for 15 year trends; 1900–1951 for 62 year trends). He then determines the extent to which the across-ensemble variations in ΔF, α and κ contribute to the ensemble spread of GMST trends. Marotzke’s main factual conclusions follow from these three factors explaining little of the ensemble spread of GMST 15-year trends, with the majority being attributed to internal variability, whilst for 62-year periods starting from the 1920s on variations in ΔF, or ERF trends, dominate with variations in model feedback α and ocean heat uptake efficiency κ having almost no effect.
Flaws in Marotzke’s methods
To a physicist, the result that variations in model α and κ have almost no effect on 62-year trends is so surprising that the immediate response should be: ‘what has Marotzke done wrong?’
Some statistical flaws are self evident. Marotzke’s analysis treats the 75 model runs as being independent, but they are not. Only 18 models are analysed, and only one set of predictor variables is used per model. The difference between temperature simulations from each individual run by a model with multiple runs and the run-ensemble mean for that model is accordingly noise that one could not expect to be explained by the regression. The use of all the individual runs invalidates the simple statistical model used and the error estimates derived from it. Also, moving from equation (1) to (3) above will have made the errors correlated with the predictor variables, biasing the coefficient estimates. Uncertainty in the values of the parameters α and κ and in the forcing time series is also ignored. As I show later, uncertainty in κ, at least, is large. And in equation (1) α and κ appear only in terms of their sum. Allowing a separate predictor variable for each of them may result in part of the internal variability being misallocated.
However, there is an even more fundamental problem with Marotzke’s methodology: its logic is circular.
The ΔF values were taken from Forster et al (2013)[v]. For each model, historical/RCP scenario time series for ΔF were diagnosed by Forster et al using an equation of the form:
. ΔF = α ΔT + ΔN (4)
where ΔT and ΔN are the model-simulated GMST and TOA radiative imbalance respectively, and α is the model feedback parameter, diagnosed in the same paper.
Moreover, κ had been diagnosed from the model transient climate response[vi] (TCR) as . Therefore, the denominator in equation (1) is simply
, termed ρ (rho) in Forster et al (2013). Note that F2xCO2, the ERF from a doubling of CO2 concentration, does not take a standard value (3.71 Wm‑2 per IPCC AR5) but is a diagnosed value that differs significantly between models.
One can therefore restate the ‘physical foundation of energy balance’, with added random term representing internal variability, (equation (1)) as:
. ΔT = (α ΔT+ ΔN ) / ρ + ε (5)
As is now evident, Marotzke’s equation (3) involves regressing ΔT on a linear function of itself. This circularity fundamentally invalidates the regression model assumptions. Accordingly, reliance should not be placed on any of the results in the Nature paper. That is particularly the case for the 62-year trend results, where the offending, non-exogenous ΔF’ term dominates the ensemble spread of GMST trends for start years from the 1920s on.
Since the ΔF predictor variable is a linear function of the response variable ΔT, which becomes larger relative to noise as the start year progresses, it is hardly surprising that the across-ensemble variations of ΔF are the main contributor to the ensemble spread of GMST 62-year trends starting from the 1920s onwards. As the start date progresses the intermodel variation in 62-year trends in ΔF is increasingly determined by intermodel variation in trends in α ΔT: ΔN trends are noisy but intermodel variation in trends in ΔN is of lesser relative importance for later start years. However, since ΔT is not an exogenous variable, domination in turn of intermodel variation in trends in GMST by variation in trends in ΔF tells one nothing reliable about the relative contributions of forcing, feedback and ocean heat uptake efficiency to the intermodel spread in GMST trends.
Examining the effects of the circularity in Marotzke’s method
One could, at the expense of changing the error characteristics somewhat, rearrange (5) to eliminate ΔT from the RHS and remove the circularity, which (since κ = ρ – α) results in simply[vii]
. ΔT = ΔN / κ + ε (6)
However, Marotzke does not do so, and in any case this equation only deals with the element of forcing that is associated with ocean etc. heat uptake, not with the (larger) element associated with increasing GMST, and it does not include α.
I’ll stick with Marotzke’s approach for the time being but derive a regression equation from (5) via a similar expansion to that employed by him, here keeping the two terms comprised in ΔF separate but not splitting the ρ term between α and κ. Linearly expanding (5) yields:
which on keeping only the lowest terms but separating the influence of the and
terms leads to a regression equation of this form:
I have carried out a regression analysis based on equation (8) using the same set of models. I used the run-ensemble mean where a model had multiple runs, not all the individual runs. The justification for not using all the separate runs was given earlier. Using run-ensemble means will however result in model internal variability not being fully represented in the regression residuals.
Over early, middle and late 15-year periods within the 1900–2012 analysis period, the intermodel spread in GMST trend is dominated by the term; internal variability (assessed from the variance not explained by the regression fit) is small. Over the earliest and latest 62-year periods (1900–1961 and 1951–2012) the
term continues to be dominant but less so, with a greater amount of unexplained variance. The other two terms explain very little of the intermodel spread, save for modest contributions from the ρ term in the 62-year trend cases. There is little point in examining more than two or three historical 62-year trend cases, as results from periods with substantial overlap are far from independent.
The results from this rejigged regression show that the apparent internal variability shrinks greatly when different coefficients are permitted for the two terms in the diagnosed forcing. And one can actually get even better fits for all periods by regressing using just and
terms.
However, none of the analysis examined so far is valid, because in all of it ΔT appears on both sides of the equation – whether explicitly as in equation (8) or, as in Marotzke’s paper, concealed within ΔF – so there is circularity involved either way. Naturally, if one separates out, as in equation (8), the predictor variable term in which the response variable appears simply multiplied by a parameter – – from an associated noisy term with little explanatory power –
– the regression will explain more of the variability in the response variable. But the fact that the
term – the only exogenous part of
– has no significant explanatory power suggests that Marotzke’s 62-year period results likely just reflect the decline in the intermodel variation in the noisy
term relative to that in the circular
term as the period considered ends closer to 2012.
Another reason why Marotzke’s approach is doomed
Another major problem with this type of attribution approach, even if the circularity could be removed by somehow diagnosing ΔF differently and other statistical problems dealt with, is that the underlying assumption that the previously diagnosed α and κ values for individual models are realistic enough to use in equation (1), or in its circularity-free reduced κ-only version (6), appears to be false.
I have compared κ values based on the ratio of ΔN and ΔT trends over 1951–2012 from the model-simulations with the values used by Marotzke, which as explained were diagnosed in Forster et al 2013 by a quite different method. The ΔN / ΔT trend-based estimates vary from 0.54 times to 2.48 times those Marotzke uses; for only five models are the two estimates the same within 10%. Estimates of κ based on the 2005–2066 period under the RCP8.5 scenario, which provides a strong greenhouse gas forcing ramp with little influence from variations in aerosol forcing, range from 0.46 times to 1.09 times those Marotzke uses, and from 0.18 times to 1.75 times those estimated from changes over 1951–2012. And estimates of κ based on changes in the rate of simulated ocean heat uptake during 1961–2005,[viii] rather than simulated TOA radiative imbalance, are substantially different again. It seems doubtful that estimates of α values would be robust enough either.
With this degree of apparent variation in κ when estimated by different methods and over different periods, one would expect equation (6) to have very little explanatory power (regressing ΔT on ΔN / κ). And that is indeed the case. The intermodel spread in GMST trend is dominated by internal variability over both 15 and 62-year periods, whether towards the start or end of the analysis period. The more valid, circularity-free, version of the surface energy-balance equation is useless for investigating the intermodel spread in GMST trends. The same applies when using a regression equation based on (6) but separating the and κ terms, leading to this form:
Conclusions
I have shown that there are no valid grounds for the assertions made in the paper that ‘For either trend length, spread in simulated climate feedback leaves no traceable imprint on GMST trends’ and that ‘The claim that climate models systematically overestimate the response to radiative forcing from increasing greenhouse gas concentrations therefore seems to be unfounded’.
Marotzke conclusion that for periods ending in the last few decades the non-noise element of 62-year GMST trends in models is determined just by their ERFs is invalid, since he hasn’t used an exogenous ERF estimate. Indeed, if the models are working properly, their GMST trends must logically also reflect their feedback strengths and their ocean heat uptake efficiencies.
The interesting question is how much the large excess of model ensemble-mean simulated GMST trends relative to observed trends over the satellite era is attributable to respectively: use of excessive forcing increases; inadequate feedback strength (excessive ECS); inadequate ocean heat uptake efficiency; negative internal variability in the real climate system; and other causes. The Marotzke and Forster paper does not bring us any closer to providing an answer to this question. It certainly does not show the claim that climate models systematically overestimate the response to radiative forcing from increasing greenhouse gas concentrations to be unfounded.
One of Marotzke’s conclusions is, however, quite likely correct despite not being established by his analysis: it seems reasonable that differences between simulated and observed trends may have been dominated – except perhaps recently – by random internal variability over the shorter 15-year timescale.
Gordon Hughes had some pithy comments about the Marotzke and Forster paper:
The statistical methods used in the paper are so bad as to merit use in a class on how not to do applied statistics.
All this paper demonstrates is that climate scientists should take some basic courses in statistics and Nature should get some competent referees.
The paper is methodologically unsound and provides spurious results. No useful, valid inferences can be drawn from it. I believe that the authors should withdraw the paper.
Nicholas Lewis
[i] Jochem Marotzke & Piers M. Forster. Forcing, feedback and internal variability in global temperature trends. Nature, 517, 565–570 (2015)
[ii] This so-called kappa model does not respect conservation of energy over long periods, but as Marotzke says it is a reasonable approximation (at least in climate models) over periods of one to several decades.
[iii] Extended from 2005 to 2012 using, it appears, the RCP4.5 scenario runs.
[iv] The NorESM1-M model was incorrectly shown as not having forcing estimates available, but does seem to have been included in the models used.
[v] Forster, P. M. et al. Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models. J. Geophys. Res. 118, 1–12 (2013).
[vi] The rise in GMST over a ~70 year period during which CO2 concentration increases at 1% pa, thereby doubling.
[vii] Although it would arguably be more logical to regard ΔN rather than ΔT as the response variable in this equation.
[viii] Derived from IPCC AR5 Fig.9.17.b
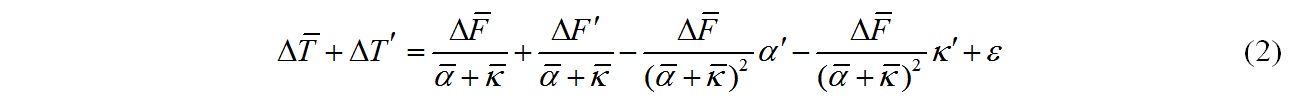
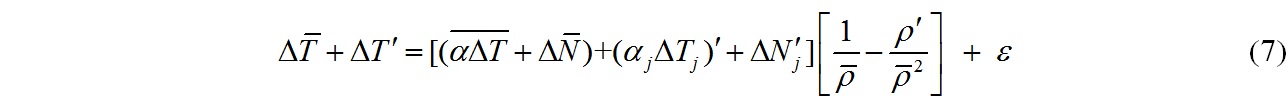
Leave A Comment