A pdf copy of this article is available here
Key points
- The herd immunity threshold (HIT) depends positively on the basic reproduction number R0 and negatively on heterogeneity in susceptibility.
- Since neither of the factors on which the HIT depends are fixed, the HIT is not fixed either.
- R0 depends on biological, environmental and sociological factors; colder weather and the evolution of more transmissible strains likely both increase R0; more (less) cautious behaviour and social distancing / restrictions on mixing reduce (increase) R0.
- Second waves were due primarily to changes in these factors increasing R0 and thus the HIT from below to above the existing level of population immunity.
- Heterogeneity in susceptibility is partly biological, but social connectivity differences are key.
- The effect of heterogeneity in susceptibility on the HIT can be represented by a single parameter λ.
- λ will always exceed 1 (its level in a homogeneous population); pre-epidemic λ may be ~4. The higher λ is, the lower the HIT for any given R0.
- The natural infection HIT is hence bound to be below the level of {1 – 1/R0} quoted by ‘experts’.
- Government restrictions reduce λ as well as R0, so the HIT falls less than it would if λ were fixed.
- The final size of an uncontrolled epidemic will substantially exceed the HIT, due to overshoot, so high reported seroprevalence levels can be consistent with a much lower HIT.
Introduction
Many people, myself included, thought that in the many regions where COVID-19 infections were consistently reducing during the summer, indicating that the applicable herd immunity threshold had apparently been crossed, it was unlikely that a major second wave would occur. This thinking has been proved wrong. In this article I give an explanation of why I think major second waves have happened.
The herd immunity threshold (HIT) for a disease epidemic is the proportion of the population needing to have been infected, and thereby no longer susceptible to infection, before the rate of new infections starts to decline. The HIT depends both on the basic reproduction number for infections (R0) – the number of other people that at the start of an epidemic an infected person will on average infect – and the degree of heterogeneity in individuals’ likelihood of being infected (their susceptibility). That likelihood in turn depends on both their social connectivity and biological susceptibility to infection. Neither R0 nor the degree of heterogeneity in susceptibility is fixed in value, so the HIT is not fixed either.
Changes in population behaviour – whether arising from government interventions or in response to increasing disease incidence – affect both R0 and heterogeneity in susceptibility. In addition, R0 (which is proportional to how readily infection is on average transmitted between individuals) may vary seasonally, and change as the virus or other infectious organism mutates.
The resurgence of COVID-19 infections in a second wave after the summer ended is almost certainly due to some combination of the foregoing sociological and biological factors. It has been claimed that the influence of weather on its transmission is relatively minor,[1] and it has so far proved difficult to detect seasonality for COVID-19.[2] However, common colds caused by other coronaviruses are highly seasonal and I now think that it is reasonable to work on the basis that COVID-19 shares that behaviour.
I focus in this article on the mathematical dependence of the HIT to R0 and heterogeneity in susceptibility, and on the factors influencing those controlling variables. I also touch on difference between the HIT and the final size of an uncontrolled epidemic. I discuss in an appendix how, in my view, changes in the factors influencing R0 and heterogeneity in susceptibility likely shaped the evolution of the epidemic in western Europe
How the HIT varies with R0 and population heterogeneity
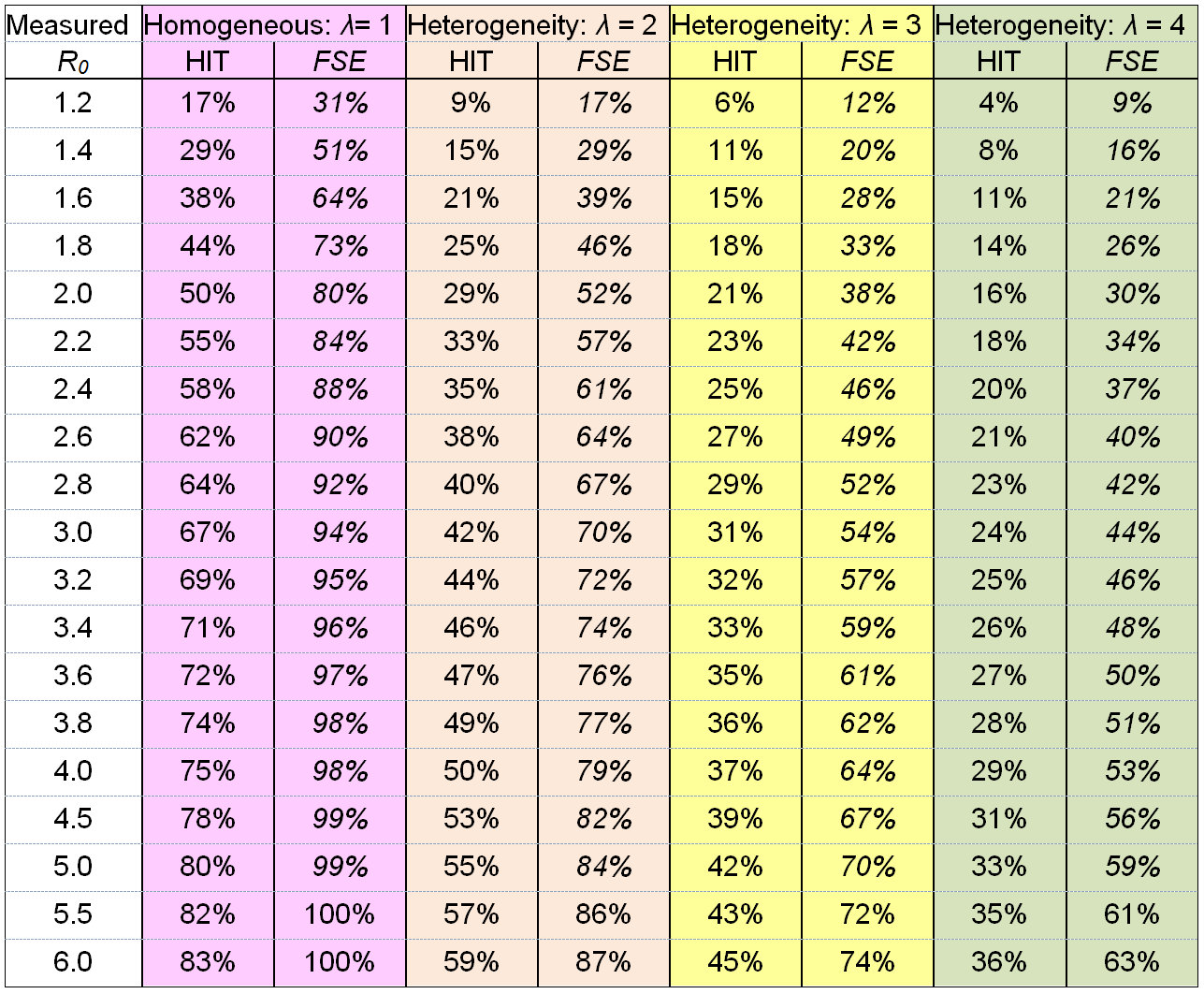
Table 1 illustrates how the herd immunity threshold varies with R0 and population heterogeneity in susceptibility to infection. The effect of such heterogeneity on transmission of infection and on the HIT can be represented by a single parameter λ, the heterogeneity factor (Tkachenko et al. 2020)[3], which is a function of population variability in both social connectivity and in biological susceptibility.[4] The reproduction number at any time, Rt, and the HIT are related as follows to R0 and λ:
Rt = R0 × Sλ
HIT = 1 – (1/R0)1/λ
where S is the proportion of the population that remains susceptible to infection. For a homogeneous population, these formulae reduce to the classical results Rt = R0 × S and HIT = 1 – 1/R0. With heterogeneity in susceptibility to infection, Rt falls more than pro rata to the susceptible proportion S decreases. Initially, Rt falls λ times as fast with S as in the homogeneous case.
Note that an epidemic takes some time to die out after the HIT is reached, since at that point many people will be infected and will go on to infect others, albeit at a declining rate. Therefore, the final size of the epidemic (FSE) – the attack rate (the ultimate proportion of the population that has been infected) – will exceed the HIT. The columns to the right of each HIT column show (in italics) the FSE if social and biological factors remain unchanged throughout the epidemic.[5] As shown in a previous article,[6] well timed short term restrictions to reduce transmission as the HIT is approached can prevent the FSE from significantly overshooting the HIT.
Table 1. Relationship of each of the herd immunity threshold (HIT) and the final size of the epidemic (FSE) with the basic reproduction number R0, at varying levels of heterogeneity factor λ that arises from heterogeneity in susceptibility (assumed gamma-distributed) across the population, from none (λ = 1) to an estimated normal level (λ = 4). The FSE values assume that the same R0 and λ value applied throughout the epidemic.
Since a person’s social connectivity, which reflects their average rate of contacts with others, equally affects their infectivity, variability in it has a more powerful effect than variability in biological susceptibility.[7] Note that heterogeneity in infectivity that is uncorrelated with susceptibility does not affect the overall progression of an established, large epidemic, although it may affect smaller scale features such as clustering of cases.
For a population that is homogeneous in both biological and social components of susceptibility, λ = 1 (pink columns). In that case, the ‘classical’ formula HIT = 1 – 1/ R0 is valid. This formula also applies to immunity gained through vaccination at random, since such vaccination – unlike natural disease progression – does not preferentially confer immunity on individuals who are more susceptible to infection (and also more likely to infect others).
Analyses of contact networks indicate that, in normal circumstances, the coefficient of variation (standard deviation / mean) for social connectivity in a population is about 1, while biological susceptibility is likely to have a coefficient of variation of about 1/3 or more (Tkachenko et al). Use of those figures implies that λ = 4 (green, rightmost columns).
The effect of government social distancing measures on R0 and the heterogeneity factor
It has been estimated that, prior to significant social distancing taking place, 80% to 90% of all transmission of infection is caused by circa 10% of infected individuals, often at superspreading events where a large number of people are present. When restrictions on gatherings, bars and other venues are introduced, non-household social mixing generally is reduced and superspreading opportunities fall even further, while household mixing will be little affected. The result will be a reduction in R0, but also reduced heterogeneity in social connectivity and hence λ. A further reduction in both these factors can be expected to occur when a lockdown (stay-at-home order) is introduced.
The effects of such government measures, for a range of resulting R0 values, are illustrated by the two middle sets of columns. These both assume the same 1/3 coefficient of variation for biological susceptibility, but a reduction in the coefficient of variation for social connectivity to 0.625, resulting in λ = 3 (yellow columns) or to 0.25, resulting in λ = 2 (salmon columns).
Even in the absence of legal restrictions being imposed, people can be expected to significantly change their behaviour when an epidemic involving severe disease takes hold. The resulting reduction in λ, for any given resulting reduction in R0, might however be less than under an enforced reduction in mixing, since more gregarious people may be less cautious and reduce their high social mixing proportionately less than more cautious, less gregarious people do – the opposite relationship to that arising from restrictions on gatherings, bars and other venues.
How a high seroprevalence level can arise even in the presence of substantial heterogeneity
It might be thought that a high attack rate is incompatible with significant population heterogeneity in susceptibility and hence a moderate HIT. An attack rate of 76% has been claimed for the city of Manaus.[8] However, the weighted measured seroprevalence on which that estimate was based was not from a random sample nor representative of the population,[9] and never exceeded 44%[10]. A random population survey found seroprevalence in Manaus to be only between one-quarter one-third the level claimed in the foregoing study, casting severe doubt on its claim.[11]
The first mentioned study also estimated that in or just after mid-March, near the start of the epidemic in Manaus, Rt – which at that point would not have been far short of R0 – was approximately 2.5, suggesting R0 was in the 2.6 to 2.8 range. The extent of physical distancing that they estimated applied then was moderate, similar to that near the end of the main epidemic. In a relatively poor city like Manaus with household and transport crowding it seems quite likely that in normal circumstances there is lower population heterogeneity in social connectivity than in a high income city, indicating an heterogeneity factor λ perhaps more like 3 than 4 (yellow not green columns). And under moderate social distancing the heterogeneity factor λ might be closer to 2 than 3. For an R0 of 2.6, λ = 2 implies an HIT of 38% but a final epidemic size (FSE) of 64%[12]. Even at λ = 3, the FSE would be 49% (with an HIT of 27%).[13]
To summarize, it seems doubtful that the attack rate in Manaus in fact exceeded 50% – it may have been no more than 20-25% – and an attack rate of 50% is fully compatible with the HIT being below 30%.
Appendix – Changes in R0 and population heterogeneity during the epidemic
The following discussion, which represents my semi-quantitative broad brush analysis of what has occurred, relates primarily to the progress of the epidemic in western Europe. However, it may also be somewhat applicable to the north east United States, where the epidemic took off only slightly later than in western Europe and where the seasonal variation in climate is also large.
In the initial stages of the first wave, which generally started in major cities, in early spring 2020, infections appear to have been doubling every three days or so prior to governments imposing restrictions or people becoming significantly more cautious. Depending on the assumed distribution of the generation interval (from one infection to those it directly leads to), that implies an R0 value of between 2 and 4.[14] I will assume a middle of the range R0 value of 3 for illustrative purposes. That would imply a HIT of 67% for a homogeneous population, reducing to 24% for a population with the highest degree of heterogeneity illustrated in Table 1, which might be expected to apply before people started behaving more cautiously and mixing less.
When people started mixing less, voluntarily or by government fiat, R0 would have reduced, but as discussed above λ will also have fallen. The combined effect of these changes can be visualised as moving diagonally upwards and leftwards in Table 1, from the green columns to the yellow columns and then to the salmon columns. The resulting reduction in the HIT would therefore be somewhat smaller than that implied by the reduction in R0 alone.
By late spring or early summer the first wave had largely faded, and it generally continued to decline after restrictions on mixing were at least partially relaxed. As summer progressed, people’s behaviour unsurprisingly returned closer to pre-epidemic norms. I will assume for illustrative purposes that the yellow columns (λ = 3) were representative of that period. Since by midsummer the epidemic appears to have been declining even where only a minor first wave had occurred, it seems that R0 must generally have declined to 1 or below, so that population immunity levels would everywhere have exceeded the HIT (which is only positive if R0 > 1).
As autumn arrived, infections and then serious illness started to rise again, although where testing was increasing the rise may have been exaggerated. It follows that R0 must have risen again, resulting in the HIT increasing to above the level of population immunity. An obvious explanation for the rise in R0 is seasonally reduced sun and cooler weather, with more contact occurring indoors, where almost all COVID-19 transmission appears to take place. A major increase in mixing among young people as school and, particularly, university terms started likely also boosted R0 and the level of infections in the autumn; young adults have generally had the highest incidence rates during the second wave.[15] In some places the rise in infections appears to have occurred slightly earlier, perhaps as a result of holidaymakers returning infected from areas where COVID-19 was more prevalent.[16]
Initially it seemed that some large cities where a significant proportion of the population had been infected in the first wave might be spared, but in most cases the increase in R0 evidently became sufficiently large to raise the HIT to above the level of population immunity. As a result of increasing infections, government-imposed restrictions were generally increased, which as well as reducing R0 will also have reduced the heterogeneity factor λ. This can be visualised as a move diagonally upwards from the yellow columns to the salmon columns. Those actions appear typically to have pushed Rt down to about 1, or slightly lower, which in the presence of a reasonable degree of existing population immunity implies an R0 level significantly above 1. With reduced heterogeneity, the existing level of population immunity causes a lesser reduction in Rt, relative to R0, but Rt will still be a smaller fraction of R0 than the proportion of the population that remains susceptible to infection.
In the UK, and possibly various other countries, a new lineage (B.1.1.7) of the SARS-CoV-2 virus has now emerged[17] and grown faster than existing ones, as discussed in a previous article[18]. Since writing that article, some further data has provided less indirect evidence that B.1.1.7 is 25–50% more infectious than pre-existing variants.[19] On the other hand, recent data from the regions where B.1.1.7 has become dominant suggests that it may now be growing no faster than other variants.[20] It has been suggested that the fast growth in the regions where B.1.1.7 now dominates may have been at least partly due to it spreading there in schools.[21] However, making for illustrative purposes the assumption that B.1.1.7 is actually 25–50% more infectious, R0 will have been increasing, perhaps typically reaching somewhere in the range1.5 to 2.0 once B.1.1.7 becomes the dominant variant, if R0 was previously in the 1.2 to 1.4 range.
Tougher restrictions that have been introduced in a number of countries in response to infection rates increasing, whether due to the spread of the B.1.1.7 lineage, to cold winter weather or to greater mixing, will have reduced population heterogeneity in social connectivity further. In these circumstances, is unclear whether existing levels of population immunity will suffice to prevent further growth of the B.1.1.7 lineage, or the rather similar one that has emerged in South African, even with severe restrictions being introduced. However, increased population immunity resulting from some combination of further spread of infections and vaccination programmes, the combination varying from one country and region to another, should bring COVID-19 epidemics under control within the next few months.
Nicholas Lewis 10 January 2021
[1] “All pharmaceutical and non-pharmaceutical interventions are currently believed to have a stronger impact on transmission over space and time than any environmental driver.” Carlson CJ, Gomez AC, Bansal S, Ryan SJ. Misconceptions about weather and seasonality must not misguide COVID-19 response. Nature Communications. 2020 Aug 27;11(1):1-4. https://doi.org/10.1038/s41467-020-18150-z
[2] Engelbrecht FA, Scholes RJ. Test for Covid-19 seasonality and the risk of second waves. One Health. 2020 Nov 29:100202. https://doi.org/10.1016/j.onehlt.2020.100202
[3] Tkachenko, A.V. et al.: Persistent heterogeneity not short-term overdispersion determines herd immunity to COVID-19. medRxiv 29 July 2020 https://doi.org/10.1101/2020.07.26.20162420 They use the term ‘immunity factor’ for λ. Equations [11)], [12] and [13] and intervening paragraph. I adopt their assumption that there is negligible correlation across the population between biological susceptibility to infection and either social connectivity or biological infectivity.
[4] I make from here on the common assumption that a gamma distribution can well represent variation within the population in both social connectivity and biological susceptibility, on which basis λ = (1 + 2 × CVs2) × (1 + CVb2) where CVs and CVb are respectively the social and biological coefficients of variation (standard deviation / mean) for the population.
[5] The FSE (1 – S∞) depends on the sum of the squared coefficients of variation η = CVs2 + CVb2 as well as on λ. It is given by the solution to the equation S∞ = (1 + R0 η [1–S∞λ–η]/[ λ–η])–1/η. See Tkachenko et al. equation [17].
[6] https://nicholaslewis.org/when-does-government-intervention-make-sense-for-covid-19/
[7] Variability in infectivity that is uncorrelated with susceptibility in the population has no overall effect in a sizeable epidemic.
[8] Buss, Lewis F., et al. “Three-quarters attack rate of SARS-CoV-2 in the Brazilian Amazon during a largely unmitigated epidemic.” Science (2020).
[9] It was a convenience sample, comprised entirely of blood donors.
[10] That maximum seroprevalence estimate was adjusted upwards to 52% to account for test for sensitivity and specificity. The attack rate estimate further assumed that antibodies would no longer be detectable in a proportion of previously infected individuals.
[11] Hallal, P.C. et al:SARS-CoV-2 antibody prevalence in Brazil: results from two successive nationwide serological household surveys. Lancet, 8(11), e1390-e1398,, September 2020 https://doi.org/10.1016/S2214-109X(20)30387-9
[12] Actually slightly lower, as the stricter social distancing measures in the middle part of the epidemic would have reduced the excess of the FSE over the HIT.
[13] If R0 = 2.0, which is possible if a shorter estimate of the generation interval is used, the corresponding FSE sizes would be 52% or 38%, with the HIT being respectively 29% or 21%.
[14] Assuming a gamma distributed generation interval with a mean in the range 4 to 6.5 and a coefficient of variation between 0.37 and 0.74.
[15] Aleta A, Moreno Y. Age differential analysis of COVID-19 second wave in Europe reveals highest incidence among young adults. medRxiv. 13 November 2020. https://doi.org/10.1101/2020.11.11.20230177
[16] It is also possible that, notwithstanding a published finding to the contrary, the A20.EU1 variant that was brought back from Spain by people infected on holiday there may have been somewhat more infectious than existing variants.
[17] Other evidence that has now become available suggests that a similar variant arose in Italy prior to B.1.1.7 being detected in the UK.
[18] https://nicholaslewis.org/the-relative-infectivity-of-the-new-uk-variant-of-sars-cov-2/
[19] The observed 50–70% increase in weekly growth rate corresponds to roughly a 25–50% increase in infectivity (and hence in R0), assuming a generation interval with a 4–6 day mean and a reasonable CV, if R0 was previously not substantially above 1.
[20] https://www.ons.gov.uk/peoplepopulationandcommunity/healthandsocialcare/conditionsanddiseases/adhocs/12722estimatesofcovid19casesto02januaryforenglandregionsofenglandandbycasescompatiblewiththenewvariant
[21] Loftus (2021, Jan. 1). Neurath’s Speedboat: Did the new variant of COVID spread through schools? Retrieved from http://joshualoftus.com/posts/2021-01-01-did-the-new-variant-of-covid-spread-through-schools/
Great article as usual! Do you have an estimate for what R_0 would be for the Fall/Winter? I’ve been using 2.5 as a placeholder…
In large cities R0 might be higher than 2.5 with no changes in behaviour or rules since a year ago, since (judging from early epidemic growth rates) R0 was almost certainly >2, perhaps as high as 3, in many countries last March and climatic influences are more favourable for transmission now.
Outside large cities R0 will be lower and 2.5 might be reasonable for the no behavioral changes case.
It is difficult to tell the current R0 since behavioural changes will have reduced R0 substantially, for the time being. And the buildup of herd immunity will have reduced Rt (which can be directly estimated) to an uncertain amount below R0.
Nic, what’s your opinion of this paper by Ioannidis and colleagues? Their claim is that mitigations help reduce R(t) but that there’s no evidence for additional benefit from moving to relatively mild government action and into hard lockdowns. https://onlinelibrary.wiley.com/doi/epdf/10.1111/eci.13484
There are many confounding influences on the growth of case numbers as well as non-pharmaceutical interventions (NPIs), as the authors acknowledge. I think that makes drawing robust conclusions about the effects of mild NPIs and the additional effects of lockdowns difficult. But I think the overall thrust of their conclusions is probably right – that is, mild NPIs had a significant effect (although the difference between mandatory and advisory mild NPIs could be small) but going to a lockdown did not have a significant extra effect. As they say, substantial changes in behaviour would have occurred evem without any NPI.
I do however think that their use of case data is not ideal. I’m with Flaxman et al. in preferring the use of deaths data. I’d also like to have seen explicit, probabilistic, modelling of the delay between an NPI being made and it affecting growth in cases, and also allowance being made for the effect of growing population immunity on growth rate in cases, either assuming a reasonable level of heterogeneity in suscptibility or estimating it.
Great article – thanks. You mention the finding that younger people have a higher incidence of cases with respect to their proportion of the population. I have observed the same increased incidence (30%-50% higher) in the data for my locality (Colorado, US), since the beginning of the epidemic. Couldn’t this over-proportion be used as a predictor of HIT? In other words, the younger cohort should reach HIT sooner, and the proportion of cases in that cohort should decrease to below their proportion of the population at that time. I don’t yet see such a decrease in the data that I am following, but it seems that it would have to happen at some point.
I think that the higher incidence in younger people (e.g., aged up to 50) is largely a reflection of heterogeneity in social connectivity – they tend to mix with more other people than do old people. So it should already be reflected in estimates of the HIT that allow suitably for heterogeneity and that relate to the % of the total population that have been infected.
Got it. My error was to assume that this over-proportion would eventually revert to the mean, which isn’t necessarily true – it can persist till herd immunity. Thanks!
We took a hard look at the winter surge in California and came to the conclusion that Winter connectivity levels exceeded those at the onset of the outbreak … our results are largely consistent with the high level conclusions here. Our model includes both connectivity and susceptibility probability distributions as well as dynamic models for connectivity over time by age group. https://covidplanningtools.com/understanding-the-california-winter-surge/
Thanks for your comment and link. I meant to reply earlier, but I’m afraid I got sidetracked. I will look at your model and article.